Um poligono do plano Oxy tem área s.
A função f:R^2->R^2 tal que:
f(x,y)=(2x+y,x+2y) o tranforma num polígonode área:
a) s
b) 2s
c) 4s
d) s/2
e) 3s



 cuja área é
cuja área é 
 , cuja área é
, cuja área é 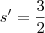


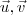 vetores de um espaço vetorial bidimensional representados no plano Oxy, tais que:
vetores de um espaço vetorial bidimensional representados no plano Oxy, tais que: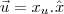
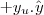
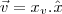

 e
e  são lados de um dos triângulos, então o módulo do produto vetorial
são lados de um dos triângulos, então o módulo do produto vetorial  é numericamte igual ao dobro da área do triângulo supracitado.
é numericamte igual ao dobro da área do triângulo supracitado.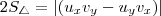
 a área seria:
a área seria: 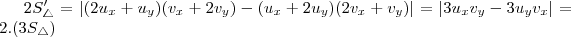

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

