por Carolziiinhaaah » Sex Jul 09, 2010 22:22
por Carolziiinhaaah » Sex Jul 09, 2010 22:22
Calcule o determinante da matriz:
 gabarito
gabarito: zero.
Pergunta: é baseada nas propriedades de determinantes ou é braçal mesmo?
Se alguém puder resolvê-la

-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Tom » Sáb Jul 10, 2010 01:50
por Tom » Sáb Jul 10, 2010 01:50
Sabemos que se

é uma matriz quadrada de ordem

e uma de suas fileiras, isto é, linha ou coluna, é igual a combinação linear de outras fileiras paralelas, então o determinante da matriz é igual a
zero.
Na matriz em questão:

Percebemos que

, veja um caso genérico:

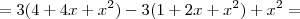

Portanto,
o determinante é nulo !!!Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- poliedro
por Gir » Ter Jan 12, 2010 10:59
- 2 Respostas
- 1667 Exibições
- Última mensagem por Gir

Sex Jan 15, 2010 10:16
Geometria Espacial
-
- Poliedro
por flavio2010 » Seg Jun 28, 2010 23:47
- 1 Respostas
- 23080 Exibições
- Última mensagem por vyhonda

Dom Jul 04, 2010 01:01
Geometria Espacial
-
- Poliedro
por aline2010 » Qui Ago 26, 2010 20:38
- 0 Respostas
- 1157 Exibições
- Última mensagem por aline2010

Qui Ago 26, 2010 20:38
Geometria Espacial
-
- poliedro
por creberson » Ter Set 18, 2012 10:20
- 3 Respostas
- 2731 Exibições
- Última mensagem por Renato_RJ

Ter Set 18, 2012 13:39
Geometria Espacial
-
- (POLIEDRO) Provar que o no. é inteiro
por Carolziiinhaaah » Sex Fev 04, 2011 15:39
- 5 Respostas
- 2766 Exibições
- Última mensagem por Carolziiinhaaah

Sáb Fev 05, 2011 13:59
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 é uma matriz quadrada de ordem
é uma matriz quadrada de ordem  e uma de suas fileiras, isto é, linha ou coluna, é igual a combinação linear de outras fileiras paralelas, então o determinante da matriz é igual a zero.
e uma de suas fileiras, isto é, linha ou coluna, é igual a combinação linear de outras fileiras paralelas, então o determinante da matriz é igual a zero.
 , veja um caso genérico:
, veja um caso genérico: