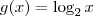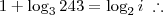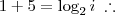por Anderson POntes » Qui Jul 08, 2010 20:52
por Anderson POntes » Qui Jul 08, 2010 20:52
Boa noite sou novo aqui e gsotaria de saber a resolução da questaoa abaixo e, pois estou estudando para um concurso e nao tive ainda nenhum raciocinio que chegasse a resolução da questao!
Quando os alunos perguntaram ao professor qual era a
sua idade, ele respondeu: “Se considerarmos as funções
f(x) = 1 + log3x e g(x) = log2x, e a igualdade
g(i) = f(243), i corresponderá à minha idade, em anos.”
Quantos anos tem o professor?
(A) 32
(B) 48
(C) 56
(D) 60
(E) 64
Agradeço desde já..
-
Anderson POntes
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jul 08, 2010 17:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico eletrotécnica
- Andamento: formado
 por Anderson POntes » Qui Jul 08, 2010 21:45
por Anderson POntes » Qui Jul 08, 2010 21:45
Alguem?
-
Anderson POntes
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Jul 08, 2010 17:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico eletrotécnica
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [função logarítimica] ajuda?
por danielleecb » Seg Set 26, 2011 18:09
- 2 Respostas
- 1658 Exibições
- Última mensagem por danielleecb

Qui Set 29, 2011 16:03
Funções
-
- [Deviravas] Função Logaritimica
por dehcalegari » Sex Jun 21, 2013 11:40
- 0 Respostas
- 917 Exibições
- Última mensagem por dehcalegari

Sex Jun 21, 2013 11:40
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADAS] Dúvida em exercício com Função Logaritimica
por dehcalegari » Sex Jun 07, 2013 10:52
- 0 Respostas
- 869 Exibições
- Última mensagem por dehcalegari

Sex Jun 07, 2013 10:52
Cálculo: Limites, Derivadas e Integrais
-
- Equação logarítimica
por Danilo Dias Vilela » Qua Ago 18, 2010 16:03
- 1 Respostas
- 1172 Exibições
- Última mensagem por Molina

Qua Ago 18, 2010 16:28
Logaritmos
-
- (CAP)Equação logaritimica
por natanskt » Qui Out 14, 2010 12:21
- 3 Respostas
- 1910 Exibições
- Última mensagem por natanskt

Qui Out 14, 2010 17:28
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.