 por liliars » Qua Jul 07, 2010 16:34
por liliars » Qua Jul 07, 2010 16:34
Preciso de ajuda com o seguinte limite:
![\lim_{x \rightarrow\infty}\frac{\sqrt[]{x² + 2x}}{5x - 1} \lim_{x \rightarrow\infty}\frac{\sqrt[]{x² + 2x}}{5x - 1}](/latexrender/pictures/c44936b0a3696b2c238a5a5e5c97833a.png)
Sei que tem de multiplicar pela raiz/raiz, mas depois, não consigo eliminá-la do denominador.
Alguém?

-
liliars
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 07, 2010 16:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por liliars » Qua Jul 07, 2010 16:36
por liliars » Qua Jul 07, 2010 16:36
* x² aí em cima, hihi.
-
liliars
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 07, 2010 16:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por Tom » Qui Jul 08, 2010 01:20
por Tom » Qui Jul 08, 2010 01:20
Desejamos obter:

Ora,
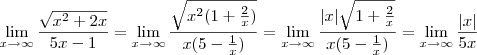
Liliars, como você não definiu se o limite é tendendo a

ou

, vou fazer os dois casos:
Para
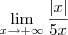
; como
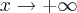
decorre em

e assim,
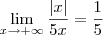
Para
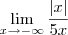
; como
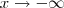
decorre em
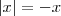
e assim,
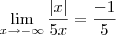
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por liliars » Sex Jul 09, 2010 02:16
por liliars » Sex Jul 09, 2010 02:16
muito melhor! obrigada!
-
liliars
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 07, 2010 16:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por elinesena » Sáb Nov 24, 2012 15:22
por elinesena » Sáb Nov 24, 2012 15:22
Boa tarde! ^^
Alguém poderia me explicar porque o x fica em módulo?
Grata
-
elinesena
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Nov 24, 2012 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Contábeis
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITES][ Indeterminação com Raiz no numerador]
por maurosilva7 » Qua Abr 22, 2015 19:42
- 2 Respostas
- 3064 Exibições
- Última mensagem por maurosilva7

Dom Jul 26, 2015 20:54
Cálculo: Limites, Derivadas e Integrais
-
- [limite] Raiz no numerador
por emanes » Qua Ago 22, 2012 09:08
- 1 Respostas
- 1791 Exibições
- Última mensagem por e8group

Qua Ago 22, 2012 10:32
Cálculo: Limites, Derivadas e Integrais
-
- Limite raiz numerador
 por Darkila » Qua Abr 27, 2016 15:49
por Darkila » Qua Abr 27, 2016 15:49
- 3 Respostas
- 4631 Exibições
- Última mensagem por Ninno Nascimento

Seg Mai 02, 2016 20:50
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] Com a raiz no numerador e denominador!!
por mih123 » Seg Ago 27, 2012 03:52
- 6 Respostas
- 5295 Exibições
- Última mensagem por mih123

Ter Ago 28, 2012 15:09
Cálculo: Limites, Derivadas e Integrais
-
- Limite para resolver com raíz no numerador e denominador
por jmoura » Sex Mar 23, 2012 23:20
- 2 Respostas
- 9035 Exibições
- Última mensagem por MarceloFantini

Sáb Mar 24, 2012 08:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x \rightarrow\infty}\frac{\sqrt[]{x² + 2x}}{5x - 1} \lim_{x \rightarrow\infty}\frac{\sqrt[]{x² + 2x}}{5x - 1}](/latexrender/pictures/c44936b0a3696b2c238a5a5e5c97833a.png)


![\lim_{x \rightarrow\infty}\frac{\sqrt[]{x² + 2x}}{5x - 1} \lim_{x \rightarrow\infty}\frac{\sqrt[]{x² + 2x}}{5x - 1}](/latexrender/pictures/c44936b0a3696b2c238a5a5e5c97833a.png)




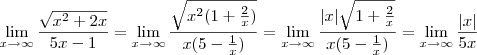
 ou
ou  , vou fazer os dois casos:
, vou fazer os dois casos: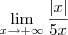 ; como
; como 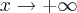 decorre em
decorre em  e assim,
e assim, 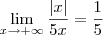
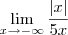 ; como
; como 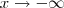 decorre em
decorre em 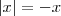 e assim,
e assim, 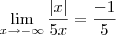



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.