 por gtrbarata » Ter Jul 06, 2010 20:04
por gtrbarata » Ter Jul 06, 2010 20:04
Olá, meu professor deixou um exercicio para a sala tentar resolver, mais estamos com dificuldades, gostaria de uma explicação.
o enunciado é o seguinte :
Dado sec x = 9/4, sendo x<= 3pi/2 <= 2pi, determine as demais funções.
( dado secante x 9 sobre 4 x menor ou igual a 3pi sobre 2 que é menor ou igual a 2pi, determine as demais funcoes.)
-
gtrbarata
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jul 06, 2010 19:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
 por Tom » Qua Jul 07, 2010 00:39
por Tom » Qua Jul 07, 2010 00:39
Imagino que a pergunta seja a respeito das outras funções trigonométricas; então vamos calculá-las:
Se
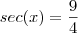
, então
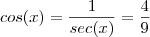
Usando o Teorema Fundamental da Trigonometria,
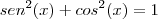
, então
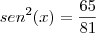
e assim,
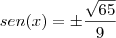
Mas, como
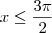
então

Como
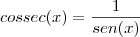
, temos que :
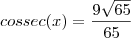
Além disso,
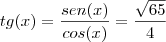
Por fim, como

, então:
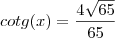
Eis as funções:


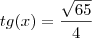
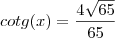
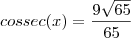
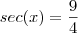
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- trigonometria-funçoes inversas
por henrique_mat » Seg Ago 23, 2010 18:57
- 4 Respostas
- 2609 Exibições
- Última mensagem por henrique_mat

Ter Ago 24, 2010 20:59
Trigonometria
-
- Funções Envolvendo Trigonometria
por ElizabethS2 » Qua Dez 08, 2010 12:14
- 1 Respostas
- 2093 Exibições
- Última mensagem por Elcioschin

Qua Dez 08, 2010 15:26
Trigonometria
-
- TRIGONOMETRIA - CÁLCULO COM FUNÇÕES INVERSAS
por emsbp » Qui Abr 19, 2012 19:13
- 4 Respostas
- 1953 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:14
Trigonometria
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3594 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3428 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


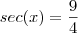 , então
, então 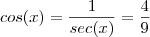
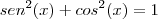 , então
, então 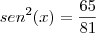 e assim,
e assim, 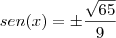
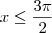 então
então 
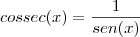 , temos que :
, temos que : 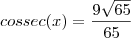
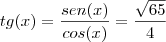
 , então:
, então: 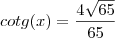




 , avisa que eu resolvo.
, avisa que eu resolvo.

