 por CloudP4 » Qui Jun 24, 2010 00:02
por CloudP4 » Qui Jun 24, 2010 00:02
Queria saber como faço para identificar uma função continua, vou pegar um exemplo:
f(x) = { x + 4, se x < 2
x - 1, se x >= 2}
Aproveitando o embalo, como faço para achar o calor de L e M para que a função seja continua
f(x) = { x³ - 2x² - 5x + 6 / x² - x - 6, se x é diferente de -2 e 3
L , se x = -2
M, se x = 3}
PS: Não consegui escrever a fórmula pelo Latex
-
CloudP4
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 07, 2010 23:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por Tom » Sex Jul 02, 2010 02:57
por Tom » Sex Jul 02, 2010 02:57
Na funçao que você citou:
Se

, então
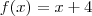
e a função é uma reta, portanto contínua.
Se

, então
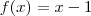
e a função é uma reta, portanto contínua.
Se antes de

e depois de

a função é contínua, basta avaliar se

é um ponto de descontinuidade, isto é, se o limite

quando

tende a

pela direita é diferente do limite quando

tende a

pela esquerda.
Ora, o limite pela esquerda:
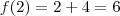
usando a lei para valores menores que

O limite pela direita:

usando a lei para valores maiores que

Como os limites são diferentes, então a função é descontínua sendo

a abicissa do ponto de descontinuidade.
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função continua
por Amparo » Dom Mar 09, 2008 16:14
- 1 Respostas
- 3922 Exibições
- Última mensagem por admin

Qui Mar 13, 2008 12:52
Funções
-
- proporçao continua
por hevhoram » Qua Jun 16, 2010 22:19
- 2 Respostas
- 2050 Exibições
- Última mensagem por hevhoram

Qua Jun 16, 2010 23:42
Álgebra Elementar
-
- função continua
por alexandreredefor » Dom Jul 17, 2011 18:23
- 4 Respostas
- 3184 Exibições
- Última mensagem por Molina

Seg Jul 18, 2011 11:42
Cálculo: Limites, Derivadas e Integrais
-
- Frações Contínua
por rhodry » Qua Nov 16, 2011 18:52
- 10 Respostas
- 12588 Exibições
- Última mensagem por matheus_vitorf

Qua Jul 26, 2017 15:31
Funções
-
- Fração continua
por Rosana Vieira » Sex Mar 02, 2012 00:48
- 1 Respostas
- 2881 Exibições
- Última mensagem por timoteo

Sex Mar 02, 2012 02:09
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , então
, então 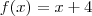 e a função é uma reta, portanto contínua.
e a função é uma reta, portanto contínua. , então
, então 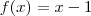 e a função é uma reta, portanto contínua.
e a função é uma reta, portanto contínua. e depois de
e depois de  quando
quando  tende a
tende a  pela direita é diferente do limite quando
pela direita é diferente do limite quando 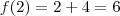 usando a lei para valores menores que
usando a lei para valores menores que  usando a lei para valores maiores que
usando a lei para valores maiores que 