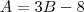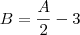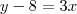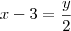por gustavowelp » Qua Jun 30, 2010 18:57
por gustavowelp » Qua Jun 30, 2010 18:57
Esse deve ser um assunto fácil, mas me confundi ao tentar resolver...
Em um dos departamentos de uma instituição de ensino, há um lote contendo pastas nas cores verde e vermelha. Sabe-se que há 8 pastas vermelhas a menos do que o triplo de pastas verdes, e há 3 pastas verdes a menos do que a metade de pastas vermelhas. Nessas condições, o total de pastas desse lote é:
A resposta é 48.
Mas pensei assim:
3 x Pverde = Pvermelha - 8
Pvermelha / 2 = Pverde - 3
Até aí acho estar correto.
Mas resolvendo:
Pvermelha = 2.(Pverde - 3) = 2.Pverde - 6
3 x Pverde = ( 2.Pverde - 6) - 8
3.Pverde = 2.Pverde - 6 - 8 => Pverde = -14 ????? (tem que ser o módulo?)
Já me perdi aí!!!
Depois:
Pvermelha / 2 = Pverde - 3
Substituindo:
Pvermelha = 2 . (-14 - 3) = 2 * (17 ou 11)???
Aí deu problema.
Se alguem puder ajudar...
Obrigado!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por Douglasm » Qua Jun 30, 2010 19:25
por Douglasm » Qua Jun 30, 2010 19:25
Olá Gustavo. Chamando o número de pastas vermelhas de
A e o número de pastas verdes de
B, encontramos as seguintes equações:
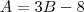
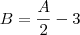
Resolvendo o sistema encontramos:


-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Qua Jun 30, 2010 19:27
por DanielFerreira » Qua Jun 30, 2010 19:27
Em um dos departamentos de uma instituição de ensino, há um lote contendo pastas nas cores verde e vermelha. Sabe-se que há 8 pastas vermelhas a menos do que o triplo de pastas verdes, e há 3 pastas verdes a menos do que a metade de pastas vermelhas. Nessas condições, o total de pastas desse lote é:
A resposta é 48.
pastas verdes: x
pastas vermelhas: y
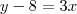
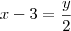
y = 3x + 8
y = 2x - 6
3x + 8 = 2x - 6
x = - 14y = 3 * - 14 + 8
y = - 42 + 8
y = - 34x = 14
y = 34
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.