![\lim_{x \rightarrow 1} \frac{\sqrt[]{x} - 1}{\sqrt[]{2x+3} - \sqrt[]{5}} \lim_{x \rightarrow 1} \frac{\sqrt[]{x} - 1}{\sqrt[]{2x+3} - \sqrt[]{5}}](/latexrender/pictures/e05a915229d57e3b888e016056a6d24c.png)
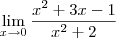
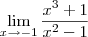
![\lim_{x \rightarrow 7} \frac{\sqrt[]{x} - \sqrt[]{7}}{\sqrt[]{x + 7} - \sqrt[]{14}} \lim_{x \rightarrow 7} \frac{\sqrt[]{x} - \sqrt[]{7}}{\sqrt[]{x + 7} - \sqrt[]{14}}](/latexrender/pictures/cca90b1c02de48af919ea504cc0bb43e.png)
E quem puder me explicar, como identifico o limite pelo método intuitivo, conforme mostra a img abaixo:

Desculpe um pouco o excesso, mas essas são mihas dúvidas no momento.
Obs: Ainda não cheguei a ver derivada.

![\lim_{x \rightarrow 1} \frac{\sqrt[]{x} - 1}{\sqrt[]{2x+3} - \sqrt[]{5}} \lim_{x \rightarrow 1} \frac{\sqrt[]{x} - 1}{\sqrt[]{2x+3} - \sqrt[]{5}}](/latexrender/pictures/e05a915229d57e3b888e016056a6d24c.png)
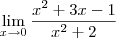
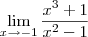
![\lim_{x \rightarrow 7} \frac{\sqrt[]{x} - \sqrt[]{7}}{\sqrt[]{x + 7} - \sqrt[]{14}} \lim_{x \rightarrow 7} \frac{\sqrt[]{x} - \sqrt[]{7}}{\sqrt[]{x + 7} - \sqrt[]{14}}](/latexrender/pictures/cca90b1c02de48af919ea504cc0bb43e.png)



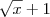 ), e depois embaixo pelo conjugado também. Verá que o (x-1) pode ser cancelado, e aí o limite não é mais indeterminado. O quarto é feito de maneira análoga.
), e depois embaixo pelo conjugado também. Verá que o (x-1) pode ser cancelado, e aí o limite não é mais indeterminado. O quarto é feito de maneira análoga.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes

 .
.



