 por Fernanda Lauton » Seg Jun 28, 2010 10:58
por Fernanda Lauton » Seg Jun 28, 2010 10:58

Por favor, como resolver:
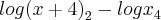
= 2

Primeiro eu sei que como as bases são diferentes eu tenho que torná-las iguais. assim eu utilizo a fórmula de mudança de base, então tenho:
para colocar tudo na base '2':
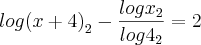

então temos no divisor que:

agora substituindo temos:
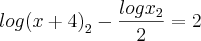

agora passando o 2 para o segundo membro, multiplicando tenho:

.
A partir daqui eu não sei mais como seguir em frente, só sei que a resposta é s= 4
Alguém poderia me ajudar

Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por Fernanda Lauton » Seg Jun 28, 2010 15:24
por Fernanda Lauton » Seg Jun 28, 2010 15:24
Sim entendo, agora sei fazer mas para que eu não volte a fazer o mesmo erro gostaria de saber porque não seria possivel passar o 2 multiplicando sendo que esta operação é possível

passando o 2 multiplicando daria algo diferente


Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por Douglasm » Seg Jun 28, 2010 16:03
por Douglasm » Seg Jun 28, 2010 16:03
Na verdade essa história de "passar o 2 para o outro lado" é só modo de dizer, isso não é realmente importante, o que é importante é fazer a operação corretamente. Veja um exemplo mais simples do seu erro:
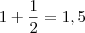
"Passando o 2 para o outro lado":

O certo é:
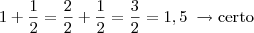
Observe agora o que você fez:

("Passando o maldito 2")

Note que para "passar o denominador multiplicando para outro lado" (insisto em dizer que o que acontece realmente é que você multiplica os dois lados da equação pelo valor em questão) TODOS os membros devem estar sobre o denominador. Então o correto fica sendo:
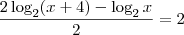

-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Fernanda Lauton » Seg Jun 28, 2010 20:18
por Fernanda Lauton » Seg Jun 28, 2010 20:18
Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por Douglasm » Seg Jun 28, 2010 20:45
por Douglasm » Seg Jun 28, 2010 20:45
Fique tranquila Fernanda. Tudo se esclarecerá. Não é uma questão de MMC. Pense bem, ao "passar o dois para o outro" lado, este 2 deve dividir todo o lado da equação, não apenas um único membro, por isso é que você tem que fazer o que fez...
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Fernanda Lauton » Ter Jun 29, 2010 09:20
por Fernanda Lauton » Ter Jun 29, 2010 09:20
Acho que tõ começando a entender... é no caso uma questão de proporcionalidade não é eu quero me livrar do 'meio' então por isso multiplico td por '2' o meio se torna um eu sumo com o denominador e tudo continua sendo proporcional não é:?:
Mas me diz uma coisa por se tratar de uma subtração porque eu não faço o MMC

Alias em que situações eu faço o MMC e quando eu faço isso

Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por Douglasm » Ter Jun 29, 2010 10:09
por Douglasm » Ter Jun 29, 2010 10:09
É isso mesmo, tudo tem que se manter proporcional (acho que esse é o melhor jeito de se entender). Bom, como já disse, não acho muito importante se prender a essa terminologia, o melhor é que você entendo o porquê de se fazer as operações. De qualquer modo, o m.m.c. vai acabar servindo para somar frações, por exemplo:

O interessante é você pesquisar um pouco sobre os assuntos que tem dificuldade e dar uma boa lida na teoria, porque realmente não tem mistério.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10722 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9734 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3317 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4615 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
-
- Problema. . .
por Fernanda90 » Qui Ago 27, 2009 20:36
- 3 Respostas
- 6538 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 22:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 Por favor, como resolver:
Por favor, como resolver: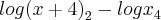 = 2
= 2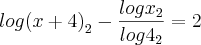
 agora substituindo temos:
agora substituindo temos: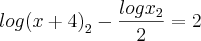
 .
.
 Por favor, como resolver:
Por favor, como resolver: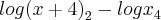 = 2
= 2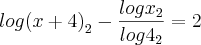
 agora substituindo temos:
agora substituindo temos: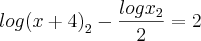
 .
.
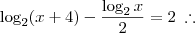



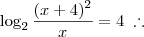
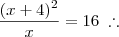
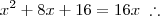





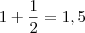

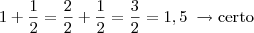


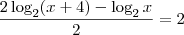


 Me desculpem a ignorância mas nunca tive uma base boa em matemática e agora estou tentando aprender
Me desculpem a ignorância mas nunca tive uma base boa em matemática e agora estou tentando aprender 







