Nessa questão, você pode fazer "no braço", o que vai te tomar algum tempo, ou você pode usar o algoritmo de eliminação de Gauss e, deste modo, encontrar rapidamente a resposta. Para não me delongar além do necessário, eu vou postar um link com a explicação do algoritmo, e demonstrar como fica a matriz já escalonada (se você usar o algoritmo aqui, logo no primeiro passo já encontrará a resposta).
O link:
http://rpanta.com/downloads/material/Gauss_01.PDFA matriz já escalonada:
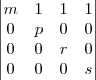
Calculando o determinante dela, do modo tradicional, rapidamente chegamos a:
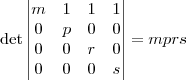
Até a próxima.
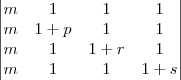
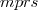

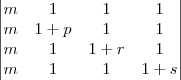
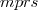

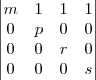
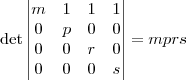



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)