 por ptt » Seg Jun 21, 2010 20:38
por ptt » Seg Jun 21, 2010 20:38
Gente, voltei a estudar a algum tempo, e achei esse fórum, oque eu mais precisava, porém, estou com dificuldade pra resolver essa inequação. Procurei como resolver essa inequação, porém nada me esclareceu a dúvida
Resolva as inequações a seguir, no universo dos números reais (U=R)
1º (x - 3)^4 > 0
2º (x - 3)^4 < 0
Por favor, me ajudem com ela, me explicando como resolver ela.
Obrigado
Edit: Tentei de tudo, porém, não consigo entender por que a resposta do livro, li tudo sobre inequações, mas não consegui ainda intender por que a resposta da primeira inequação da 3, e a segunda da zero
-
ptt
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jun 21, 2010 20:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrônica
- Andamento: formado
 por Molina » Ter Jun 22, 2010 00:19
por Molina » Ter Jun 22, 2010 00:19
Boa noite.
Obrigado por confiar em nós.
Primeiro de tudo, lembre-se que uma inequação, na maioria dos casos, o resultado é um conjunto, e não apenas um único valor.
No exercício 1, por exemplo:
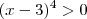
Você não vai achar apenas um valor e sim vários deles (um conjunto). Pois, você quer, os números que subtraindo 3 e elevando a 4 seja maior do que zero. Resolve-se da mesma forma que uma equação. Note que vou fazer de forma detalhada:
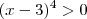
Podemos escrever essa expressão desta forma:
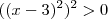
Lembre-se que qualquer número ao quadrado é maior ou igual a zero. Só será zero quando tiver
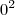
.
Mas,
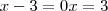
. Significa que neste valor essa expressão é igual a zero (e não maior do que zero). Então não nos importa.
A Solução então é todos os reais, menos o 3:
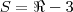
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Ter Jun 22, 2010 00:56
por MarceloFantini » Ter Jun 22, 2010 00:56
Apenas reescrevendo, pois é um conjunto solução: S =

- {3}.
E na segunda, o conjunto solução é vazio, pois não existe nenhum número real tal que elevado a quarta potência dê menor que zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matémática básica
por drea70br » Dom Out 04, 2009 20:59
- 1 Respostas
- 6171 Exibições
- Última mensagem por Elcioschin

Dom Out 04, 2009 21:10
Álgebra Elementar
-
- Operação básica
por Fernanda Lauton » Qui Jun 17, 2010 15:40
- 11 Respostas
- 6471 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 21, 2010 18:13
Álgebra Elementar
-
- Equação básica
por SaraSFT » Ter Jul 03, 2012 06:12
- 1 Respostas
- 1489 Exibições
- Última mensagem por MarceloFantini

Ter Jul 03, 2012 22:23
Matemática Financeira
-
- Dúvida básica
por SaraSFT » Ter Jul 03, 2012 06:33
- 1 Respostas
- 1318 Exibições
- Última mensagem por MarceloFantini

Ter Jul 03, 2012 22:31
Matemática Financeira
-
- definiçao basica
por giboia90 » Dom Abr 07, 2013 21:17
- 1 Respostas
- 2086 Exibições
- Última mensagem por e8group

Dom Abr 07, 2013 22:06
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


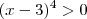
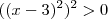
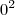 .
.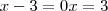 . Significa que neste valor essa expressão é igual a zero (e não maior do que zero). Então não nos importa.
. Significa que neste valor essa expressão é igual a zero (e não maior do que zero). Então não nos importa.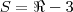

 - {3}.
- {3}.