A seguir voce tem tres afirmações .leia com atençao e marque V para verdadeiro e F para falso:
( ) O centro de uma elipseestá sempre na origem do sistema cartesiano
( ) avioes e embarcaçoes orientam -se por GPS (sistema de posicionamento global)que usa coordenadas fornecidas via satelite sobre um plano cartesiano.
( ) as seccoes conicassao:a elipse a hiperbole,a parabola, e a circunferencia



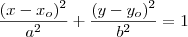 , onde
, onde 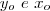 não podem ser, simultaneamente, iguais a zero.
não podem ser, simultaneamente, iguais a zero.


