Raios do círculo:
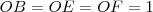
Aplicação direta do teorema de Pitágoras:

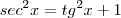

Obtemos a tangente a partir da semelhança entre os triângulos OAF e OBC, pelo caso ângulo-ângulo:
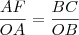
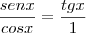

A secante, também por semelhança entre os mesmos triângulos:
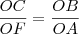

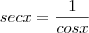
Já a cotangente, por semelhança entre os triângulos OED e OAF, também pelo caso AA pois o ângulo
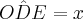 :
: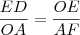


E a cosecante, também por semelhança entre os triângulos OED e OAF, segue diretamente desta relação:


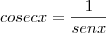



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.