x + 2y - 3z = 6
2x - y + 4z = 2
4x + 3y - 2z = 14
Algém por gentileza poderia resolver pelo método de escalonamento e cramer por favor





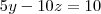
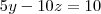
 . Isso implica que
. Isso implica que  e
e  . Portanto, as triplas ordenadas que são soluções do sistema são do tipo
. Portanto, as triplas ordenadas que são soluções do sistema são do tipo 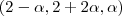 .
.

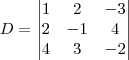
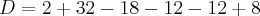
 . Como o Fantini disse, não se trata de um problema que tenha solução única, pois
. Como o Fantini disse, não se trata de um problema que tenha solução única, pois  . E como foi dito na resolução de um outro problema que você enviou, não vale a pena resolver usando a Regra de Cramer.
. E como foi dito na resolução de um outro problema que você enviou, não vale a pena resolver usando a Regra de Cramer.




Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: