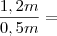por funerius » Qui Jun 10, 2010 22:21
por funerius » Qui Jun 10, 2010 22:21
Olá meu povo.. alguém pode me ajudar com estas questões?
(TFC) Em um depósito devem ser acondicionadas caixas em forma de cubo medindo externamente 50 cm de aresta ou lado da face. Considerando que se arrumaram as caixas face a face formando uma base retangular de 10 por 30 caixas e sempre com 12 caixas de altura, obtenha o volume do paralelepípedo formado, admitindo que as caixas se encaixam ao lado e em cima das outra perfeitamente, sem perda de espaço.
a) 450 m³ (resposta)
b) 360 kl
c) 288 m³
d) 240 m³
e) 150kg
Bem, se são 50cm de aresta, = 50 x 50 = 2500cm² de área
largura x comprimento x altura x 2500 = V (realmente seria essa a formula?)
10 x 30 x 12 x 2500 = 9000000 cm³ ( mas está errado, o certo é 450 m³ opção A, mas mesmo transformando p/ 9 m³, o
meu resultado continua errado...).
(Transpetro) Um pequeno aquário tem a forma de um paralelepípedo com 30 cm de altura, 50 cm de comprimento e 35 cm de largura. Tanto o fundo quanto as laterais do aquário são feitas de placas de vidro, coladas com uma cola especial. A quantidade de vidro, em cm², necessária para construir esse aquário é de:
a) 6.100
b) 6.850 (resposta)
c) 7.200
d) 7.750
e) 8.600
Bem, sendo um paralelepípedo, deve haver 2 medidas de largura, 2 de altura e 1 de comprimento já que a questão diz que não inclui o teto..
Assim: 2largura x 2altura x 1comprimento = area preenchida de vidro
70 x 60 x 35 = 147000 cm³ (bem longe da opção certa, 6850 cm²...)
(Petrobrás) Uma peça de lona retangular tem 10 m de comprimento e 1,2 m de largura. Qual é o número máximo de pedaços quadrados, de 0,25 m² de área, que podem ser cortados dessa peça?
a) 48
b) 44
c) 40 (resposta)
d) 30
e) 20
10 x 1,2 / 0,25 = 48 m (onde eu errei? a resposta era pra ser 40)
Se alguem puder me explicar, agradeço!
-
funerius
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Jun 08, 2010 17:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Comunicação
- Andamento: formado
 por Lelia » Qua Set 07, 2011 17:22
por Lelia » Qua Set 07, 2011 17:22
Olá funerius!
1 questão:
O único engano seu que esqueceu que cada cubo da altura também mede 50 cm.
De modo que o volume é: 10 . 50 . 30 . 50.12 . 50= 450 000 000cm³, que equivale a 450 m³.
2 questão:
Para tal aquário serão necessário:
1 placa de vidro de 50 por 35, ou seja, 1750cm²;
2 placas de 30 por 50, ou seja, 2 . 1500, que dá 3000 cm² e
2 placas de 30 por 35, ou seja, 2. 1050, que dá 2100cm²
Totalizando 6850cm²
Abçs
Lélia
-
Lelia
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Set 07, 2011 16:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Lelia » Qua Set 07, 2011 17:52
por Lelia » Qua Set 07, 2011 17:52
[quote="Lelia"]Olá funerius!
1 questão:
O único engano seu que esqueceu que cada cubo da altura também mede 50 cm.
De modo que o volume é: 10 . 50 . 30 . 50.12 . 50= 450 000 000cm³, que equivale a 450 m³.
2 questão:
Para tal aquário serão necessário:
1 placa de vidro de 50 por 35, ou seja, 1750cm²;
2 placas de 30 por 50, ou seja, 2 . 1500, que dá 3000 cm² e
2 placas de 30 por 35, ou seja, 2. 1050, que dá 2100cm²
Totalizando 6850cm²
3 questão:
Como a peça de lona mede 10 metros por 1,2m e os pedaços a serem cortados medem 0,25 m² de área, ou seja 0,5m de lado. Então termos no comprimento 20 quadrados e na largura 2,4 pedaços. Conclusão, terá num total 40 pedaços de lona de 0,5 por 0,5, e sobrará lona.
Para facilitar o seu entendimento desenhe o retângulo e imagine você o cortando como pede.
Abçs
Lélia
-
Lelia
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Set 07, 2011 16:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por DanielFerreira » Dom Jan 08, 2012 16:19
por DanielFerreira » Dom Jan 08, 2012 16:19
(Petrobrás) Uma peça de lona retangular tem 10 m de comprimento e 1,2 m de largura. Qual é o número máximo de pedaços quadrados, de 0,25 m² de área, que podem ser cortados dessa peça?
a) 48
b) 44
c) 40 (resposta)
d) 30
e) 20
10 x 1,2 / 0,25 = 48 m (onde eu errei? a resposta era pra ser 40)
A área do quadrado deve ser de 0,25m², então o comprimento e a largura medem 0,5m.
Sabendo que o comprimento da lona é de 10m, podemos determinar quantos
pedaços quadrados teremos no comprimento:

20
Vejamos agora quantos
pedaços quadrados teremos na largura:
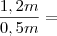
2,4;
Ou seja, 2 inteiros.
Daí,
20 * 2 =
40"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Conversão de Unidades
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- medidas
por thayna » Sáb Out 23, 2010 12:08
- 1 Respostas
- 2291 Exibições
- Última mensagem por VtinxD

Dom Out 24, 2010 00:38
Geometria Plana
-
- Medidas
por Walquiria » Dom Nov 06, 2011 19:30
- 2 Respostas
- 1973 Exibições
- Última mensagem por Walquiria

Seg Nov 07, 2011 19:03
Estatística
-
- medidas
 por ana celia » Qua Set 12, 2012 17:57
por ana celia » Qua Set 12, 2012 17:57
- 5 Respostas
- 3086 Exibições
- Última mensagem por Cleyson007

Qui Set 13, 2012 10:47
Geometria Plana
-
- Conversão de medidas
por eduardopiana » Ter Out 21, 2008 14:48
- 6 Respostas
- 7441 Exibições
- Última mensagem por Giles

Qua Out 29, 2008 23:40
Conversão de Unidades
-
- unidades de medidas!
por leandro moraes » Ter Jan 19, 2010 10:10
- 4 Respostas
- 2692 Exibições
- Última mensagem por Elcioschin

Ter Jan 19, 2010 19:41
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.