Sabe-se que o lucro total de uma empresa é dado por L(q)=R(q)-C(q), onde L é o lucro total, R a receita total e C o custo total da produção. Pede-se, numa empresa onde:
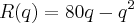
e

onde: q é a quantidade produzida. E pergunta-se:
a)o nível de produção q para que o lucro seja máximo; Resposta-> 15
b)o valor do lucro máximo. Resposta-> 410
Preciso de ajuda, pois não consegui chegar a esses valores.
Obrigado!!!


 , que nada mais é do que:
, que nada mais é do que:

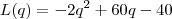
 que faz essa função ser maior possível. A ferramenta que nos permite calcular isso é o famoso
que faz essa função ser maior possível. A ferramenta que nos permite calcular isso é o famoso  (X vértice). Para usar as notações do problema, usaremos
(X vértice). Para usar as notações do problema, usaremos  que é dado pela fórmula:
que é dado pela fórmula:
 e
e  que estão na função
que estão na função 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)