 por borges25borges » Sáb Mai 31, 2008 16:43
por borges25borges » Sáb Mai 31, 2008 16:43
Exercício 7.2. É desejável aquecer 9820 lb/h de benzeno ( cp = 0,425 Btu/lb.oF ) de 80 a 120 oF utilizando tolueno ( cp = 0,44 Btu/lb.oF ), o qual é resfriado de 160 para 100 oF. Um fator de fuligem de 0,001 deve ser considerado para cada fluxo e o coeficiente global de transferência de calor "limpo" é 149 Btu/h.ft2.oF. Dispõe-se de trocadores bitubulares de 20 ft de comprimento equipados com tubos área específica de 0,435 ft2/ft.
a) Qual a vazão de tolueno necessária?
b) Quantos trocadores são necessários?
a) A vazão de tolueno pode ser obtida realizando um balanço térmico :
b) Para obter o número de trocadores é necessário calcular a área de troca de calor necessária. O MLDT do trocador é obtido assim :
Cálculo do coeficiente global considerando o fator fuligem ( sujo ) :
1/Ud = 1/Uc + Rdi +Rde
Ud = 1/149 + 0,001 + 0,001
Ud = 115 Btu/h*ft²*°F
Cálculo da área de troca de calor :
O calor trocado é igual ao calor recebido pelo benzeno, portanto :
São necessários 50,5 m2 de área de troca de calor. Como os tubos do trocador dispõem de uma área por unidade de comprimento conhecida, é possível calcular o comprimento de tubo necessário :
Como cada trocador tem tubos de 20 ft de comprimento, o número de trocadores é :
Por favor como ele chegou nesta unidade, na parte que está resolvida do cálculo do coeficiente global considerando o fator fuligem
-
borges25borges
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mai 31, 2008 16:10
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sáb Mai 31, 2008 18:42
por admin » Sáb Mai 31, 2008 18:42
Olá
borges25borges, boas-vindas!
Apenas considerando as operações matemáticas, a partir de onde você citou, sem adentrar nos detalhes físicos, pois não tenho competência para tal:
borges25borges, nestas situações onde queremos conferir a unidade obtida, meus professores do curso técnico em química sempre recomendavam "fazer as contas também com as unidades", como uma análise dimensional.
Então, vamos inserir a unidade de
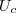
na conta, considerando que o fator seja adimensional, veja:
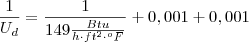
As operações com as unidades resultarão na unidade de
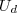
, vamos aos passos:
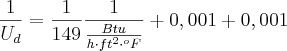
A soma dos termos adimensionais não altera a unidade, então:
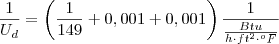
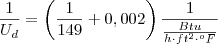
M.M.C.:
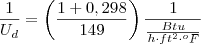
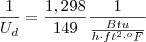
Fazendo o inverso da unidade:
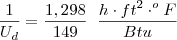
Inverso dos dois membros da equação:
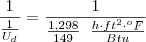
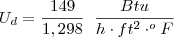
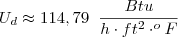
Espero ter ajudado!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por borges25borges » Sáb Mai 31, 2008 20:31
por borges25borges » Sáb Mai 31, 2008 20:31
Muito obrigado Fábio, você acaba de me salvar na prova de Fenômenos dos Transportes 2. Valeuzão, desculpe pelo jeito que digitei as fórmulas, mas não consegui usar este programa latex.
-
borges25borges
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mai 31, 2008 16:10
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Conversão de Unidades
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função exponencial] Não entendi como chegou a formula
por Leti Moura » Ter Jun 12, 2012 21:16
- 2 Respostas
- 4090 Exibições
- Última mensagem por Russman

Qua Jun 13, 2012 00:57
Funções
-
- [RESOLUÇÃO DO SISTEMA COMO ELE CHEGOU A ESSE VALOR]
 por osmarioe » Sex Mai 01, 2015 19:20
por osmarioe » Sex Mai 01, 2015 19:20
- 2 Respostas
- 2804 Exibições
- Última mensagem por osmarioe

Sáb Mai 02, 2015 14:21
Funções
-
- Como isolar PV nesta equação
por macburn » Qua Dez 15, 2010 20:22
- 1 Respostas
- 1479 Exibições
- Última mensagem por Bruno Pinheiro

Dom Dez 26, 2010 23:10
Logaritmos
-
- Produtos Notáveis - como aplicar nesta equação
por fcomex » Ter Mai 20, 2014 00:15
- 1 Respostas
- 1307 Exibições
- Última mensagem por fcomex

Ter Mai 20, 2014 01:13
Álgebra Elementar
-
- unidade imaginaria
por lieberth » Ter Jun 16, 2009 17:24
- 2 Respostas
- 1856 Exibições
- Última mensagem por Cleyson007

Qua Jun 17, 2009 10:37
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


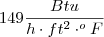

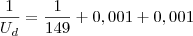
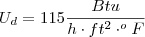
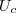 na conta, considerando que o fator seja adimensional, veja:
na conta, considerando que o fator seja adimensional, veja: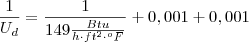
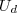 , vamos aos passos:
, vamos aos passos: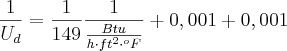
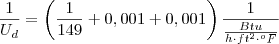
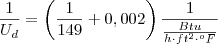
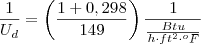
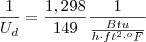
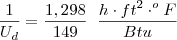
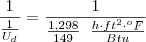
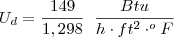
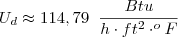



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.