Resolvi alguns exercícios porém, não consigo de forma alguma, resolve-los de forma correta. Alguém poderia me ajudar e ver o que estou fazendo de errado??
-Uma chapa metálica quadrada de lado x está se espandindo segundo a equação x= 2+t², onde a variável t representa o tempo.Determinar a taxa de variação da área desse quadrado no tempo t=2.
Bom pelo o que eu aprendi, eu teria que derivar a função e substituir 2 em t para obter a taxa de variação e como a área é igual ao lado² , ficaria assim:
x= 2+t²
x'=0+2t
x'=2t , com t=2
x'=4cm³/cm
Mas o que acontece é que a minha resposta me informa como resposta 48.Gente de onde eles tiraram esse número??!?
-Um copo de limonada a uma temperatura de 40F está em uma sala com temperatura constante de 70F.Pode-se mostrar que se a temperatura da limonada atingir 52F em uma hora, então a temperatura T da limonada como função no tempo decorrido é modelada aproximadamente pela equação T=70-30.
 , onde T está em graus F e t em horas.Qual a taxa de variação quando t=5
, onde T está em graus F e t em horas.Qual a taxa de variação quando t=5Bom aqui eu tentei resolver fazendo inicial - final dividido pelo tempo e pela derivação, mas acredito que a forma correta seja a derivação, então fiz assim:
T'=70-30.
 .(-0,5)
.(-0,5)T'=70-30.
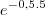 .(-0,5)
.(-0,5)T'=70-30.0,082084998.(-0,5)
T'=70-30.(-0,041042499)
T'=70+1,231274979
T'
 -71,23
-71,23A resposta correta é 1,23F/h .Por favor, alguém sabe me dizer o que estou fazendo errado??
Muito Obrigadaa




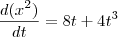
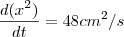 (isso se x estiver em centímetros e o tempo em segundos)
(isso se x estiver em centímetros e o tempo em segundos)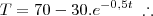

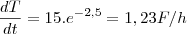


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)