 por my2009 » Qua Mai 26, 2010 18:33
por my2009 » Qua Mai 26, 2010 18:33
Boa tarde, tentei resolver esse exercicio mas nao tenho nem noção de como começa rsrs por favor me ajudem !!!
(Mackenzie) - Sejam a e b as raízes da equação x² - 3kx + k ² = 0, tais que a² + b² = 1,75.Determine k ² :
Desde ja agradeço !!!!!
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Qua Mai 26, 2010 19:55
por Molina » Qua Mai 26, 2010 19:55
Buenas!
Usando a Fórmula da Soma e do Produto de equações do 2° grau, temos que:
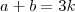 (equação 1)
(equação 1)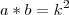 (equação 2)
(equação 2)Elevando a equação 1 ao quadrado de ambos os lado temos:
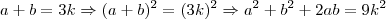
Usando a informação do enunciado, que
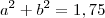
, substituimos onde paramos:
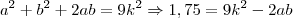
Usando a equação 2, substituimos em

:

Dúvidas?!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por my2009 » Qua Mai 26, 2010 22:58
por my2009 » Qua Mai 26, 2010 22:58
Obrigada Diego molina, me ajudou mto !!!!!! bjos
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7716 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13209 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13015 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6091 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8702 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



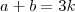 (equação 1)
(equação 1)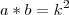 (equação 2)
(equação 2)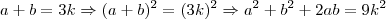
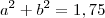 , substituimos onde paramos:
, substituimos onde paramos: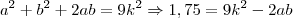
 :
:




 .
.



