 por JailsonJr » Sáb Mai 22, 2010 04:56
por JailsonJr » Sáb Mai 22, 2010 04:56
(UF-CE) A opção em que figuram as soluções da equação
![{3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]=0 {3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]=0](/latexrender/pictures/f812b014b2ecceb5b2c2df0cc5d21edc.png)
é:
Resp.: -3 e 3
------
![{3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}10 \right]=0
{3}^{{x}^{2}-8}+{log}_{10}1=0
{3}^{{x}^{2}-8}+0=0 {3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}10 \right]=0
{3}^{{x}^{2}-8}+{log}_{10}1=0
{3}^{{x}^{2}-8}+0=0](/latexrender/pictures/b2a7d4ff718e6b274de2680604164ea3.png)
Daki eu não sai ...
Quanto mais detalhado, melhor

-
JailsonJr
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Mai 14, 2010 06:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Dom Mai 23, 2010 14:05
por Molina » Dom Mai 23, 2010 14:05
JailsonJr escreveu:(UF-CE) A opção em que figuram as soluções da equação
![{3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]=0 {3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]=0](/latexrender/pictures/f812b014b2ecceb5b2c2df0cc5d21edc.png)
é:
Resp.: -3 e 3
------
![{3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}10 \right]=0
{3}^{{x}^{2}-8}+{log}_{10}1=0
{3}^{{x}^{2}-8}+0=0 {3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}10 \right]=0
{3}^{{x}^{2}-8}+{log}_{10}1=0
{3}^{{x}^{2}-8}+0=0](/latexrender/pictures/b2a7d4ff718e6b274de2680604164ea3.png)
Daki eu não sai ...
Quanto mais detalhado, melhor

Boa tarde.
O valor de
![\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right] \left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]](/latexrender/pictures/579adce8c29f52244cafb8be845518e0.png)
não é 1. Por isso não deu certo.
![\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]= \left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]=](/latexrender/pictures/c608a306c48dc04dbcdba819ab18c7bf.png)
![=\left[{log}_{10}\left(10^{\frac{1}{1000}} \right) \right]= =\left[{log}_{10}\left(10^{\frac{1}{1000}} \right) \right]=](/latexrender/pictures/e3d7821f412a09eeaf5d999b6956bc55.png)
![=\left[{\frac{1}{1000}*{log}_{10}\left(10 \right) \right]= =\left[{\frac{1}{1000}*{log}_{10}\left(10 \right) \right]=](/latexrender/pictures/28f4a05b076b0163f48757bd146d74d4.png)
![=\left[{\frac{1}{1000}*1 \right]={\frac{1}{1000}=10^{-3} =\left[{\frac{1}{1000}*1 \right]={\frac{1}{1000}=10^{-3}](/latexrender/pictures/2c85a3391b5c8df2cc46ffbec17b237a.png)
Ou seja,
![{log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]={log}_{10}\left[10^{-3}\right]=-3 {log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]={log}_{10}\left[10^{-3}\right]=-3](/latexrender/pictures/ecce13aaac954f540a0e34d45237f364.png)
Disso temos que
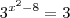
E agora é só aplicar as propriedades de exponencial e chegar no resultado correto.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por JailsonJr » Dom Mai 23, 2010 14:38
por JailsonJr » Dom Mai 23, 2010 14:38
Muiiiito Obrigado... Isso de Raiz sempre me complica :/
-
JailsonJr
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Mai 14, 2010 06:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Dom Mai 23, 2010 14:46
por Molina » Dom Mai 23, 2010 14:46
Entendo.
Quando aparece raiz eu sempre tento trabalhar ela passando pra expoente. Por exemplo:
![\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}}=\sqrt[10]{\sqrt[10]{10^{\frac{1}{10}}}}=\sqrt[10]{\left(10^{\frac{1}{10}\right)^{\frac{1}{10}}}}=\left(\left(10^{\frac{1}{10}\right)^{\frac{1}{10}\right)^{\frac{1}{10}}}=10^{\frac{1}{1000}} \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}}=\sqrt[10]{\sqrt[10]{10^{\frac{1}{10}}}}=\sqrt[10]{\left(10^{\frac{1}{10}\right)^{\frac{1}{10}}}}=\left(\left(10^{\frac{1}{10}\right)^{\frac{1}{10}\right)^{\frac{1}{10}}}=10^{\frac{1}{1000}}](/latexrender/pictures/4f632aa67c9b9b28bcf8d0bdb99538de.png)

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por JailsonJr » Dom Mai 23, 2010 14:54
por JailsonJr » Dom Mai 23, 2010 14:54
Eu achava que podia cortar tudinho kkkk'
Mas agora aprendi

-
JailsonJr
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Mai 14, 2010 06:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por jefferson0209 » Ter Set 22, 2015 17:33
por jefferson0209 » Ter Set 22, 2015 17:33
alguem me ajuda ae?
1)sendo log2=u e log3=v,determine:
a)log12
b)log15
2)calcula:
log 81+ log625-log100
.. 3 . . 5
-
jefferson0209
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Ter Set 22, 2015 15:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
 por jefferson0209 » Ter Set 22, 2015 18:32
por jefferson0209 » Ter Set 22, 2015 18:32
alguem me ajuda?
1)sendo log2=u e log3=v,determine:
a)log12
b)log15
2)calcula:
log 81+ log625-log100
.. 3 . . 5
-
jefferson0209
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Ter Set 22, 2015 15:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2567 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1845 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2723 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo
por nan_henrique » Sex Jul 09, 2010 18:38
- 1 Respostas
- 2272 Exibições
- Última mensagem por Elcioschin

Sex Jul 09, 2010 19:42
Logaritmos
-
- Logaritmo
por nan_henrique » Sáb Jul 10, 2010 12:09
- 1 Respostas
- 1491 Exibições
- Última mensagem por Douglasm

Sáb Jul 10, 2010 12:28
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]=0 {3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]=0](/latexrender/pictures/f812b014b2ecceb5b2c2df0cc5d21edc.png) é:
é:![{3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}10 \right]=0
{3}^{{x}^{2}-8}+{log}_{10}1=0
{3}^{{x}^{2}-8}+0=0 {3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}10 \right]=0
{3}^{{x}^{2}-8}+{log}_{10}1=0
{3}^{{x}^{2}-8}+0=0](/latexrender/pictures/b2a7d4ff718e6b274de2680604164ea3.png)


![{3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]=0 {3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]=0](/latexrender/pictures/f812b014b2ecceb5b2c2df0cc5d21edc.png) é:
é:![{3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}10 \right]=0
{3}^{{x}^{2}-8}+{log}_{10}1=0
{3}^{{x}^{2}-8}+0=0 {3}^{{x}^{2}-8}+{log}_{10}\left[{log}_{10}10 \right]=0
{3}^{{x}^{2}-8}+{log}_{10}1=0
{3}^{{x}^{2}-8}+0=0](/latexrender/pictures/b2a7d4ff718e6b274de2680604164ea3.png)


é:
![\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right] \left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]](/latexrender/pictures/579adce8c29f52244cafb8be845518e0.png) não é 1. Por isso não deu certo.
não é 1. Por isso não deu certo.![\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]= \left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]=](/latexrender/pictures/c608a306c48dc04dbcdba819ab18c7bf.png)
![=\left[{log}_{10}\left(10^{\frac{1}{1000}} \right) \right]= =\left[{log}_{10}\left(10^{\frac{1}{1000}} \right) \right]=](/latexrender/pictures/e3d7821f412a09eeaf5d999b6956bc55.png)
![=\left[{\frac{1}{1000}*{log}_{10}\left(10 \right) \right]= =\left[{\frac{1}{1000}*{log}_{10}\left(10 \right) \right]=](/latexrender/pictures/28f4a05b076b0163f48757bd146d74d4.png)
![=\left[{\frac{1}{1000}*1 \right]={\frac{1}{1000}=10^{-3} =\left[{\frac{1}{1000}*1 \right]={\frac{1}{1000}=10^{-3}](/latexrender/pictures/2c85a3391b5c8df2cc46ffbec17b237a.png)
![{log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]={log}_{10}\left[10^{-3}\right]=-3 {log}_{10}\left[{log}_{10}\left(\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}} \right) \right]={log}_{10}\left[10^{-3}\right]=-3](/latexrender/pictures/ecce13aaac954f540a0e34d45237f364.png)
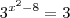



![\sqrt[10]{\sqrt[10]{\sqrt[10]{10}}}=\sqrt[10]{\sqrt[10]{10^{\frac{1}{10}}}}=\sqrt[10]{\left(10^{\frac{1}{10}\right)^{\frac{1}{10}}}}=\left(\left(10^{\frac{1}{10}\right)^{\frac{1}{10}\right)^{\frac{1}{10}}}=10^{\frac{1}{1000}} \sqrt[10]{\sqrt[10]{\sqrt[10]{10}}}=\sqrt[10]{\sqrt[10]{10^{\frac{1}{10}}}}=\sqrt[10]{\left(10^{\frac{1}{10}\right)^{\frac{1}{10}}}}=\left(\left(10^{\frac{1}{10}\right)^{\frac{1}{10}\right)^{\frac{1}{10}}}=10^{\frac{1}{1000}}](/latexrender/pictures/4f632aa67c9b9b28bcf8d0bdb99538de.png)







 .
.
 :
: