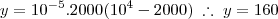por Bernar » Ter Mai 18, 2010 00:52
por Bernar » Ter Mai 18, 2010 00:52
Um lago suporta no máximo 10.000 peixes. A taxa de crescimento da população de peixes é conjuntamente proporcional ao número presente deles e à diferença entre 10.000 e o número presente.
a) Se a taxa de crescimento for de 90 peixes por semana quando 1.000 peixes estão presentes, ache a taxa de crescimento como função do número presente.
b) Ache a taxa de crescimento quando houver 2.000 peixes.
Bom, x - > número presente . y -> taxa de crescimento.
então y = x ( 10.000 - x )
se x = 10.000, y = 90
Agora não sei mais o que faço. Acho que tem que ser colocado uma constante K. Mas eu nunca sei quando deve ser usado a constante K, alguém poderia me ajudar?
-
Bernar
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Set 09, 2009 22:37
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por MarceloFantini » Ter Mai 18, 2010 20:40
por MarceloFantini » Ter Mai 18, 2010 20:40
Se
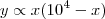
, isso implica que
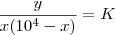
. Usando os dados do enunciado, se

, então
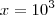
. Jogando na relação:
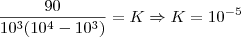
.
Logo, a expressão é:
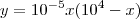
.
No segundo supostamente imponha y = 2000 e faça a conta, mas tentei no wolframalpha e deu errado. Espero que alguém consiga esclarecer.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Douglasm » Ter Mai 18, 2010 21:46
por Douglasm » Ter Mai 18, 2010 21:46
Fantini, você resolveu o problema e não colocou a resposta da última! Ele disse 2000
peixes (x) e não que a taxa de crescimento (y) era 2000. Logo:
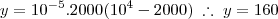
A taxa de crescimento na letra b é de 160 peixes por semana.
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Mai 18, 2010 23:28
por MarceloFantini » Ter Mai 18, 2010 23:28
Nossa, que desatenção da minha parte. Obrigado Douglas! Você tem MSN, por acaso?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5571 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4588 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5740 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3484 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2952 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


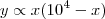 , isso implica que
, isso implica que 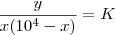 . Usando os dados do enunciado, se
. Usando os dados do enunciado, se  , então
, então 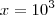 . Jogando na relação:
. Jogando na relação: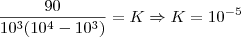 .
.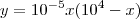 .
.