 por Neperiano » Sex Mar 19, 2010 09:38
por Neperiano » Sex Mar 19, 2010 09:38
Ola
Certo, entendi agora, é que a questão quer dizer que 3 torneiras vao encher mais rapido que 2, mas a questão esta confusa, mas mesmo assim da para responde
Se 2 torneiras vao encher em 5 horas, 4 encherão em 2h e 30 min, e 3 torneiras vao dar 3 h e 20 min, porque a difernça vai ser 1 h e 40 min de 2 torneiras para 3 e de 3 para 4,
Assim
Você tem
2 torneiras com 5 horas
4 com 2 e 30 min
Para descubrir 3 torneiras é só você tirar um numero em comum entre as duas, ou seja 3 e h e 20 min, porque vai ser 1 e 40 a mais que 2 e 30 min e 1 e 40 a menos que 5
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"






 a vazão:
a vazão: , onde
, onde  é o tempo. Percebam que não depende da vazão:
é o tempo. Percebam que não depende da vazão: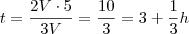


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)