 por Douglaspimentel » Sex Mar 05, 2010 12:47
por Douglaspimentel » Sex Mar 05, 2010 12:47
(MACKENZIE) Se f(x) = mx + n e f(f(x)) = 4x + 9, a soma dos possíveis valores de n é:
Tenho dificuldade nas operações do exercício.
-
Douglaspimentel
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Mar 05, 2010 12:42
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nada
- Andamento: cursando
 por Molina » Sex Mar 05, 2010 15:33
por Molina » Sex Mar 05, 2010 15:33
Douglaspimentel escreveu:(MACKENZIE) Se f(x) = mx + n e f(f(x)) = 4x + 9, a soma dos possíveis valores de n é:
Tenho dificuldade nas operações do exercício.
Boa tarde, Douglas.
Utilize as duas informações do enunciado.

e

Vamos lá:

![f(f(x))=m[f(x)]+n f(f(x))=m[f(x)]+n](/latexrender/pictures/e8d597d7d99f4fa90dcdeb77481644b5.png)
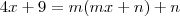
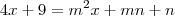
Agora note o detalhe da resolução:
Vou igualar os valores que contem x, e igualar os valores que não contem x:

Ou seja, temos dois valores para
m.
Substitua agora estes valores na outra parte que vamos igualar:
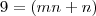
Substituindo os m's (+2 e -2) nesta equação você irá encontrar dois valores. Some-os.
O resultado dá
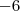
.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Paloma » Qui Mar 18, 2010 21:28
por Paloma » Qui Mar 18, 2010 21:28
Domínio de função composta!
f(x) =
![\sqrt[2]{x+1} \sqrt[2]{x+1}](/latexrender/pictures/1a4918c18d7e32bcc010b0b56b47de5f.png)
, g(x) =

D(f) = (-1,

) , D(g) = R*
Im(f) = [0,

) , Im(g) = R*
Essa foi a minha resolução da primeira parte do exercício, só que esse exercício já vem com a resposta, e o D(f) = (-1, -

), só que ae daria uma raiz de número negativo, e a minha área de estudo são só os número reais. Então acho que a minha resposta esteja certa. Se estiver errada, por favor corrijam, e as outras também.

f(g(x)) =
![\sqrt[2]{\frac{1}{x}+1} \sqrt[2]{\frac{1}{x}+1}](/latexrender/pictures/6f1994aa5204c6a5802fb993b0dee59f.png)
, o domínio de f(g(x)) consiste nos números x do domínio de g para os quais g(x) estejam no domínio de f, certo? Existe uma definição mais simples? Uma forma mais simples de achar o domínio da função composta? Ou alguém poderia me explicar isso mais claramente?

g(f(x)) =
![\frac{1}{\sqrt[2]{x+1}} \frac{1}{\sqrt[2]{x+1}}](/latexrender/pictures/ec85e04a67f07d73544a1e5397d16e4e.png)
obrigada

-
Paloma
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mar 16, 2010 20:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em Engenharia Civil
- Andamento: cursando
 por MarceloFantini » Qua Mai 12, 2010 13:42
por MarceloFantini » Qua Mai 12, 2010 13:42
Paloma, por favor poste sua dúvida em um novo tópico para evitar aglomerados de dúvidas diferentes em um mesmo lugar, facilitando a localização de todas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função composta]Achar o dominio de uma função composta
por lucasmath » Dom Abr 12, 2015 16:09
- 0 Respostas
- 2234 Exibições
- Última mensagem por lucasmath

Dom Abr 12, 2015 16:09
Funções
-
- [FUNÇÃO] NAO CONSIGO ENTENDER FUNÇÃO COMPOSTA!
por Gabriela AlmeidaS » Seg Mai 12, 2014 19:18
- 5 Respostas
- 5466 Exibições
- Última mensagem por Toussantt

Dom Jan 24, 2016 15:34
Funções
-
- Função composta
por scorpion » Sáb Out 25, 2008 11:09
- 2 Respostas
- 4205 Exibições
- Última mensagem por scorpion

Qua Out 29, 2008 14:26
Funções
-
- Função Composta
 por ginrj » Ter Jun 30, 2009 17:35
por ginrj » Ter Jun 30, 2009 17:35
- 4 Respostas
- 17049 Exibições
- Última mensagem por LuizAquino

Sáb Mar 03, 2012 14:34
Funções
-
- Função composta
 por matemalouco » Sáb Ago 15, 2009 20:43
por matemalouco » Sáb Ago 15, 2009 20:43
- 2 Respostas
- 3986 Exibições
- Última mensagem por Elcioschin

Seg Ago 17, 2009 10:26
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






![f(f(x))=m[f(x)]+n f(f(x))=m[f(x)]+n](/latexrender/pictures/e8d597d7d99f4fa90dcdeb77481644b5.png)
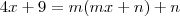
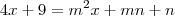

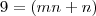
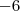 .
. 

![\sqrt[2]{x+1} \sqrt[2]{x+1}](/latexrender/pictures/1a4918c18d7e32bcc010b0b56b47de5f.png) , g(x) =
, g(x) = 
 ) , D(g) = R*
) , D(g) = R* ) , Im(g) = R*
) , Im(g) = R* ), só que ae daria uma raiz de número negativo, e a minha área de estudo são só os número reais. Então acho que a minha resposta esteja certa. Se estiver errada, por favor corrijam, e as outras também.
), só que ae daria uma raiz de número negativo, e a minha área de estudo são só os número reais. Então acho que a minha resposta esteja certa. Se estiver errada, por favor corrijam, e as outras também. 
![\sqrt[2]{\frac{1}{x}+1} \sqrt[2]{\frac{1}{x}+1}](/latexrender/pictures/6f1994aa5204c6a5802fb993b0dee59f.png) , o domínio de f(g(x)) consiste nos números x do domínio de g para os quais g(x) estejam no domínio de f, certo? Existe uma definição mais simples? Uma forma mais simples de achar o domínio da função composta? Ou alguém poderia me explicar isso mais claramente?
, o domínio de f(g(x)) consiste nos números x do domínio de g para os quais g(x) estejam no domínio de f, certo? Existe uma definição mais simples? Uma forma mais simples de achar o domínio da função composta? Ou alguém poderia me explicar isso mais claramente? 
![\frac{1}{\sqrt[2]{x+1}} \frac{1}{\sqrt[2]{x+1}}](/latexrender/pictures/ec85e04a67f07d73544a1e5397d16e4e.png)




