(UERJ) Dado que
 é a medida de um ângulo agudo com
é a medida de um ângulo agudo com 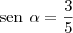 , o valor da expressão
, o valor da expressão 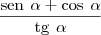 é:
é: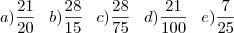
minha resolução:
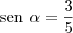
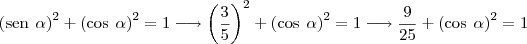
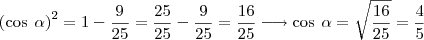
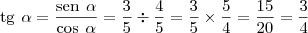
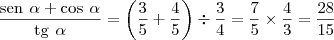
Eu a resolvi e achei o resultado
 , letra b, mas para resolver esta questão eu tive de presumir que o ângulo
, letra b, mas para resolver esta questão eu tive de presumir que o ângulo  pertence a um triângulo, e necessariamente um triângulo retângulo, pois usei o teorema de Pitágoras pra resolver a questão, daí me surgiram as dúvidas:
pertence a um triângulo, e necessariamente um triângulo retângulo, pois usei o teorema de Pitágoras pra resolver a questão, daí me surgiram as dúvidas:Somente os triângulos retângulos possuem razões trigonométricas como seno, co-seno e tangente?
Por que o coseno que poderia ser negativo ou positivo é necessariamente positivo?
Já que se usa Pitágoras na resolução desta questão o ângulo citado obrigatoriamente deve permanecer a um triângulo retângulo ou a um círculo trigonométrico?




 .
.



