Olá, querido professor, tudo bem?
Estou estudando e me deparei com essa questão, gostaria de saber se o procedimento que adotei para resolvê-la se está correto.
A altura média do tronco de certa espécie
de árvore, que se destina à produção de madeira, evolui,
desde que é plantada, segundo o modelo matemático
h(t)= 1,5 + log3 (t +1), com h(t) em metros e t em
anos. Se uma dessas árvores foi cortada quando seu
tronco atingiu 3,5 m de altura, o tempo (em anos) transcorrido
do momento da plantação até o do corte foi de:
a) 9 b) 8 c) 5 d) 4 e) 2
Observação: h(t)= 1,5 + log de (t+1) na base 3.
Eu a resolvi assim: 3,5= 1,5 + log3 (t+1) Peguei o 1,5 que está depois da igualdade e passei para antes da igualdade com o sinal inverso. 3,5 - 1,5= log3 (t+1)
2,0= log 3 (t+1) Peguei a base (o número 3) e elevei ao 2 que está antes da igualdade, ficando 9= t+1, obtendo o valor de 8 para t.
Peço desculpa por ter que explicar tudo escrito, é porque não consegui fazer no site, peço sua compreensão. Qualquer dúvida, é só postar que explico o que fiz.
Um abraço.










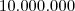 – é dez vezes dez, sete vezes seguidas, ou seja, dez à potência 7, ou seja,
– é dez vezes dez, sete vezes seguidas, ou seja, dez à potência 7, ou seja, 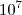 . Uma operação inversa é o logaritmo na base 10, ou seja,
. Uma operação inversa é o logaritmo na base 10, ou seja,  , que, conhecido o número dez milhões, determina qual a potência de 10 que resulta nele.
, que, conhecido o número dez milhões, determina qual a potência de 10 que resulta nele.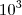 . Usa-se ainda uma escala logarítmica para definir o pH de substâncias, coeficiente que caracteriza a condição mais ácida ou mais básica de soluções. Também populações de microorganismos podem variar exponencialmente, tornando a escala logarítmica igualmente conveniente em Biologia.
. Usa-se ainda uma escala logarítmica para definir o pH de substâncias, coeficiente que caracteriza a condição mais ácida ou mais básica de soluções. Também populações de microorganismos podem variar exponencialmente, tornando a escala logarítmica igualmente conveniente em Biologia.
 .
.
 :
: