1ª Num regime de captalização composta, o montante M, resultante da aplicação de um capital C à taxa percentual i, por n períodos, é dado pelo lei
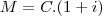 . Assim, dados M, C e n a taxa i pode ser calculada pela expressão:
. Assim, dados M, C e n a taxa i pode ser calculada pela expressão:a)
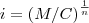
b)
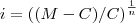
c)

d)

e)

nessa expressão eu já tentei substituir parte da formula pela formula completa do juros
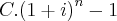 e não consegui já tentei assim tbem
e não consegui já tentei assim tbem ![\sqrt[n]{\frac{M}{C}}=\sqrt[n]{{(1+i})^{n}}\Rightarrow
\frac{{M}^{\frac{1}{n}}}{{C}^{\frac{1}{n}}}=1+i \sqrt[n]{\frac{M}{C}}=\sqrt[n]{{(1+i})^{n}}\Rightarrow
\frac{{M}^{\frac{1}{n}}}{{C}^{\frac{1}{n}}}=1+i](/latexrender/pictures/29db5880c11c19600f6260975b94e515.png)
e parei aqui pq a cabeça ta fervendo isso pq ainda tem mais outras 2 questões que vou perguntar depois.
obrigado desde já.




