 por RJ1572 » Qui Abr 08, 2010 23:22
por RJ1572 » Qui Abr 08, 2010 23:22
Boa noite.
Não entendi como se fazer este problema.
Alguém pode me ajudar na resolução?
A função F(X) = X^(2) + bx + c, se anula para X=R ou X= 3R. Determine R sabendo que o valor mínimo de F(X) é -9.
A resposta do gabarito é: R= 3 ou R=-3.
-
RJ1572
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Fev 26, 2010 13:00
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Sex Abr 09, 2010 00:53
por Molina » Sex Abr 09, 2010 00:53
RJ1572 escreveu:Boa noite.
Não entendi como se fazer este problema.
Alguém pode me ajudar na resolução?
A função F(X) = X^(2) + bx + c, se anula para X=R ou X= 3R. Determine R sabendo que o valor mínimo de F(X) é -9.
A resposta do gabarito é: R= 3 ou R=-3.
Boa noite.
A maior complicação deve ser o enunciado. Acredito que quando ele dz que
se anula, nada mais é que
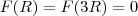
. O valor mínimo é o
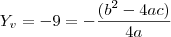
. Como pelo enunciado

esta fórmula fica reduzida a

Mas ainda não consegui passar disso

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por RJ1572 » Sex Abr 09, 2010 10:34
por RJ1572 » Sex Abr 09, 2010 10:34
Consegui.
36 = b^2 -4c
b^2 = 4c + 36
(r + r^2)^2 = 4 (r . r^2) + 36
..... e por ai vai.
Obrigado.
-
RJ1572
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Fev 26, 2010 13:00
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Elcioschin » Sex Abr 09, 2010 13:22
por Elcioschin » Sex Abr 09, 2010 13:22
Vou mostrar a solução partindo do cálculo correto do Molina: b² - 4c = 36
Relações de Girard:
x' + x" = -b/a ----> R + 3R = - b/1 -----> b = - 4R
x'*x" = c/a ------> R*3R = c/1 -----> c = 3R²
b² - 4c = 36 ----> (-4R)² - 4*(3R²) = 36 ----> 4R² = 36 ----> R² = 9 ---> R = 3 ou R = - 3
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida Função
por vb_evan » Sáb Jul 03, 2010 09:18
- 4 Respostas
- 2707 Exibições
- Última mensagem por vb_evan

Qua Jul 07, 2010 09:35
Funções
-
- Função - puc-mg dúvida
por gustavoluiss » Sáb Jan 08, 2011 17:07
- 10 Respostas
- 5364 Exibições
- Última mensagem por Renato_RJ

Sáb Jan 08, 2011 22:49
Funções
-
- Duvida no zero da função
por igorcalfe » Sex Mar 11, 2011 18:14
- 2 Respostas
- 1810 Exibições
- Última mensagem por igorcalfe

Ter Mar 15, 2011 23:35
Sistemas de Equações
-
- Função - Exp e Log - Dúvida!
por jamiel » Seg Jun 27, 2011 23:55
- 0 Respostas
- 5757 Exibições
- Última mensagem por jamiel

Seg Jun 27, 2011 23:55
Funções
-
- Função - Exp e Log - Dúvida 2 !
por jamiel » Ter Jun 28, 2011 01:25
- 0 Respostas
- 1290 Exibições
- Última mensagem por jamiel

Ter Jun 28, 2011 01:25
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



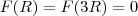 . O valor mínimo é o
. O valor mínimo é o 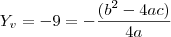 . Como pelo enunciado
. Como pelo enunciado  esta fórmula fica reduzida a
esta fórmula fica reduzida a 



