 por geriane » Ter Abr 06, 2010 00:20
por geriane » Ter Abr 06, 2010 00:20
Em uma cabine de um estádio de futebol, um computador registra todos os lances de uma partida. Em um desses lances, Zaqueu cobrou uma falta, fazendo a bola descrever um arco de parábola contido num plano vertical, parábola esta simétrica ao seu eixo, o qual também era vertical. A bola caiu no chão exatamente a 30m de Zaqueu. Durante o trajeto, a bola passou raspando a cabeça do juiz. O juiz, que não interferiu na trajetória da bola, tinha 1,76m de altura e estava ereto, a 8m de distância de onde saiu o chute. Desse modo, a altura máxima, em metros, atingida pela bola foi de:
a) 2,25m b) 4,13m c) 6,37m d) 9,21m e) 15,92m
-
geriane
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Sáb Abr 03, 2010 10:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: formado
 por Molina » Ter Abr 06, 2010 19:40
por Molina » Ter Abr 06, 2010 19:40
geriane escreveu:Em uma cabine de um estádio de futebol, um computador registra todos os lances de uma partida. Em um desses lances, Zaqueu cobrou uma falta, fazendo a bola descrever um arco de parábola contido num plano vertical, parábola esta simétrica ao seu eixo, o qual também era vertical. A bola caiu no chão exatamente a 30m de Zaqueu. Durante o trajeto, a bola passou raspando a cabeça do juiz. O juiz, que não interferiu na trajetória da bola, tinha 1,76m de altura e estava ereto, a 8m de distância de onde saiu o chute. Desse modo, a altura máxima, em metros, atingida pela bola foi de:
a) 2,25m b) 4,13m c) 6,37m d) 9,21m e) 15,92m
Boa tarde.
Primeiramente desenhe uma parábola onde as raízes (que cortam o eixo x) serão 0 e 30, pois é de onde a bola parte e onde ela chega. Essa parábola será côncava para baixo, já que é assim que a bola percorre sua trajetória e tem essa cara:
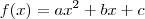
.
Temos então que quando

,

.


Então a função terá essa cara:

Agora vamos usar a informação dos pontos que temos. Quando

,

.
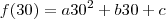
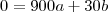
 (equação 1)
(equação 1)Outra informação do gráfico que temos é a posição do juiz. Quando

,

.
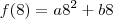
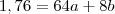 (equação 2)
(equação 2)Substituindo a equação 1 na equação 2 você encontrará

.
(o que garante a concavidade para baixo).
Com o valor de a você substitui na equação 1 e encontra

Ou seja, a equação tem essa cara:
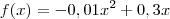
Como ele quer saber a altura máxima e a equação é simétrica, basta calcular y no ponto de
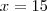
(já que é a metade de 30).
Calculando o

chegamos em
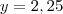
, que é a altura máxima.
Qualquer dúvida, informe!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Essa nem consegui começar
por alzenir agapito » Sex Mai 20, 2011 19:10
- 2 Respostas
- 1311 Exibições
- Última mensagem por alzenir agapito

Sáb Mai 21, 2011 10:20
Cálculo: Limites, Derivadas e Integrais
-
- [otimização] essa eu não consegui fazer, ajuda
por vinicastro » Dom Dez 16, 2012 20:30
- 1 Respostas
- 1721 Exibições
- Última mensagem por young_jedi

Dom Dez 16, 2012 22:07
Cálculo: Limites, Derivadas e Integrais
-
- Essa elipse e essa parábola se encontram?
por Gregorio Diniz » Qua Mar 12, 2014 17:00
- 2 Respostas
- 1840 Exibições
- Última mensagem por Gregorio Diniz

Qua Mar 12, 2014 18:32
Geometria Analítica
-
- Não consegui
por nayane » Qua Out 27, 2010 11:47
- 3 Respostas
- 2808 Exibições
- Última mensagem por 0 kelvin

Ter Nov 02, 2010 22:17
Estatística
-
- tentei e não consegui
por nayane » Qua Out 27, 2010 11:40
- 2 Respostas
- 1876 Exibições
- Última mensagem por nayane

Qui Out 28, 2010 20:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


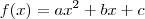 .
. ,
,  .
.


 ,
, 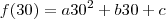
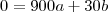

 ,
,  .
.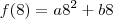
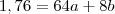
 .
.
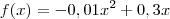
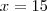 (já que é a metade de 30).
(já que é a metade de 30). chegamos em
chegamos em 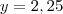 , que é a altura máxima.
, que é a altura máxima.






