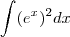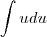por crsglc2 » Dom Abr 04, 2010 23:21
por crsglc2 » Dom Abr 04, 2010 23:21
Boa Noite!!
sou nova aqui nesse forum, achei o forum graças depois de procurar muito na web uma explicação sobre integrais
Bom a minha dificuldade é bem simples
quero apenas uma explicação mesmo, pois não entendi pelo metodo que a prof. explicou
bom...
gostaria mesmo de saber
qual a relação entre "u" "du" e "dx"
e como substituir eles corretamente no calculo
eu sei que u'=du/dx
mas oq é dx?
porq as vezes fica por exemplo du/3 ou por algum outro valor??
e como faço pra continuar a substituição???
qual a diferença entre uma integral multiplicando e uma dividindo como isso interfere em "u" "du"e "dx"
Por favor me ajudem tenho prova nessa semana disso e to super confusa
espero que eu tenha conseguido expressar +ou- minha duvida
Att.
Glau.
-
crsglc2
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Abr 04, 2010 22:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Molina » Ter Abr 06, 2010 21:58
por Molina » Ter Abr 06, 2010 21:58
Boa noite, Glau.
É mais fácil você colocar uma questão que tenha dúvida, do que explicar uma questão teórica assim. Pois há várias formas de abordar esse assunto e varia de professor para professor.
Vou dar um exemplo de substituição pra vê se melhora sua visão sobre o assunto:
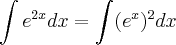
É fácil a integral de

e também é fácil integral do tipo

. Então vou fazer um substituição para poder usar essas duas integrais. Chamarei de

. Derivando de ambos os lados ficamos com
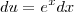
, mas

, então,

.
Voltando a expressão original:
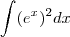

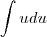

Mas

, então:

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda em Cálculo I (breve explicação)
por joana f d pinheiro » Seg Nov 16, 2009 13:18
- 3 Respostas
- 5627 Exibições
- Última mensagem por joana f d pinheiro

Qua Nov 18, 2009 22:16
Cálculo
-
- Preciso de uma explicação
por Deko » Dom Mar 28, 2010 16:33
- 1 Respostas
- 1718 Exibições
- Última mensagem por Elcioschin

Dom Mar 28, 2010 19:07
Cálculo: Limites, Derivadas e Integrais
-
- Preciso de Explicação
por andersonvendramin28 » Ter Mai 31, 2011 11:29
- 8 Respostas
- 8344 Exibições
- Última mensagem por andersonvendramin28

Qua Jun 08, 2011 15:46
Funções
-
- Explicação da tangente
por Cleyson007 » Qua Out 17, 2012 16:48
- 3 Respostas
- 3885 Exibições
- Última mensagem por Cleyson007

Qui Out 18, 2012 09:14
Trigonometria
-
- DUVIDA- EXPLICAÇÃO
por zenildo » Qui Dez 19, 2013 12:01
- 0 Respostas
- 1076 Exibições
- Última mensagem por zenildo

Qui Dez 19, 2013 12:01
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


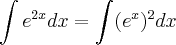
 e também é fácil integral do tipo
e também é fácil integral do tipo  . Então vou fazer um substituição para poder usar essas duas integrais. Chamarei de
. Então vou fazer um substituição para poder usar essas duas integrais. Chamarei de  . Derivando de ambos os lados ficamos com
. Derivando de ambos os lados ficamos com 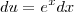 , mas
, mas  , então,
, então,  .
.