por estudandoMat » Sex Abr 02, 2010 12:38
por estudandoMat » Sex Abr 02, 2010 12:38
Olá, estou com problemas em relação a angulos formados em relogios.
1- Após às 13h, a primeira vez que os ponteiros das
horas e dos minutos formarão um ângulo de 36º será às ?
Resposta: 1h e 12 min
Bom, eu sei que o ponteiro dos minutos começa no 12h (ou 0) e o ponteiro das horas começa no 1. E que quando o ponteiro dos minutos anda, o das horas anda tb. Esse conceito eu já entendo, oque eu não consigo é calcular de maneira eficiente e rápida. Gostaria de saber uma maneira eficiente de calcular esse tipo de problema. Obrigado
-
estudandoMat
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Sex Abr 02, 2010 00:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Sex Abr 02, 2010 14:08
por Molina » Sex Abr 02, 2010 14:08
estudandoMat escreveu:Olá, estou com problemas em relação a angulos formados em relogios.
1- Após às 13h, a primeira vez que os ponteiros das
horas e dos minutos formarão um ângulo de 36º será às ?
Resposta: 1h e 12 min
Bom, eu sei que o ponteiro dos minutos começa no 12h (ou 0) e o ponteiro das horas começa no 1. E que quando o ponteiro dos minutos anda, o das horas anda tb. Esse conceito eu já entendo, oque eu não consigo é calcular de maneira eficiente e rápida. Gostaria de saber uma maneira eficiente de calcular esse tipo de problema. Obrigado
Boa tarde.
Problemas com horas são bem fáceis de resolver usando a seguinte fórmula:
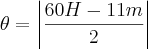
Onde

é o menor ângulo formado pelos ponteiros, H é o valor das horas (de 0 à 11), e m os minutos (de 0 a 59).
Na nossa condição,

,

e

é o que queremos descobrir:
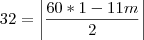
Resolva isso e encontre o valor de m, que será 12.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por estudandoMat » Sex Abr 02, 2010 14:49
por estudandoMat » Sex Abr 02, 2010 14:49
Valeu pela fórmula, Molina !!
-
estudandoMat
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Sex Abr 02, 2010 00:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relógio
por DanielFerreira » Qui Jul 30, 2009 17:46
- 1 Respostas
- 2658 Exibições
- Última mensagem por Felipe Schucman

Qui Jul 30, 2009 18:09
Trigonometria
-
- Relógio
por DanielFerreira » Qui Jul 30, 2009 17:50
- 2 Respostas
- 4073 Exibições
- Última mensagem por Elcioschin

Sáb Ago 01, 2009 13:02
Desafios Médios
-
- Desafio do relógio
por ericomoura » Ter Nov 17, 2009 12:03
- 9 Respostas
- 8315 Exibições
- Última mensagem por Dan

Qui Fev 10, 2011 12:21
Desafios Difíceis
-
- Ponteiro de relógio
por Rafael16 » Seg Mai 27, 2013 22:07
- 1 Respostas
- 2515 Exibições
- Última mensagem por Molina

Ter Mai 28, 2013 19:59
Trigonometria
-
- Ângulos no Relógio
por miguel135 » Sex Mar 28, 2014 17:02
- 11 Respostas
- 10043 Exibições
- Última mensagem por Isis

Qua Abr 30, 2014 12:02
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


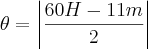
 é o menor ângulo formado pelos ponteiros, H é o valor das horas (de 0 à 11), e m os minutos (de 0 a 59).
é o menor ângulo formado pelos ponteiros, H é o valor das horas (de 0 à 11), e m os minutos (de 0 a 59). ,
,  e
e  é o que queremos descobrir:
é o que queremos descobrir: