
Gostaria de um esclarecimento sobre o procedimento que adotei para resolver o exercício acima.
No primero arco, calculei:


Minha dúvida está aqui: "Esse comprimento de 930m é o comprimento total do ângulo?" --> Acredito que seja, por isso, dividi o valor encontrado por 2, dado que o automóvel faz a curva.
No segundo arco, calculei:

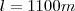
No terceiro arco, calculei:

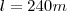 "Aqui também dividi o valor encontrado por 2, dado que o automóvel faz a curva."
"Aqui também dividi o valor encontrado por 2, dado que o automóvel faz a curva."Comprimento total: 3505m
Está correto?
Até mais.


