 por matmatco » Ter Nov 19, 2024 07:39
por matmatco » Ter Nov 19, 2024 07:39
Seja x ∈ C não nulo tal que
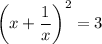
. Determine o valor da expressão

.
Notei que

.
Fiz o seguinte desenvolvimento:
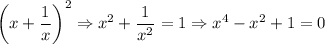
Então fiz uma substituição de variável,

, porém não possui raiz real e não consegui resolver. Depois pensei em continuar o desenvolvimento abaixo e encontrar o valor de
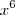
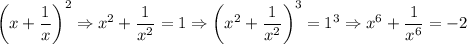
A partir daqui não consegui resolver
Editado pela última vez por
matmatco em Qua Nov 20, 2024 23:14, em um total de 1 vez.
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por DanielFerreira » Qua Nov 20, 2024 22:32
por DanielFerreira » Qua Nov 20, 2024 22:32
Olá
matmatco, meus cumprimentos!
Essa primeira parte do enunciado tá completa?
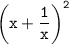
No desenvolvimento que você fez, considerou igual a três...
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por matmatco » Qua Nov 20, 2024 23:12
por matmatco » Qua Nov 20, 2024 23:12
Olá Daniel, tudo bem?
Exato, não percebi que o erro de digitação.
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por DanielFerreira » Seg Dez 16, 2024 20:30
por DanielFerreira » Seg Dez 16, 2024 20:30
Olá
matmatco, desculpe a demora! As atividades docentes do dia a dia têm me deixado bem ocupado...!
Em relação à questão, eu tentei resolvê-la da primeira vez utilizando alguns artifícios da fatoração. Mas, não consegui finalizar. Na sequência, pensei em seguir de onde vc havia parado; só que não consegui visualizar... Depois, pensei numa saída muito trabalhosa - que era determinar o valor de "x" e depois substituir na expressão

, afinal como

depois era só aplicar a
primeira fórmula de Moivre.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Seg Dez 16, 2024 20:41
por DanielFerreira » Seg Dez 16, 2024 20:41
matmatco escreveu:Seja x ∈ C não nulo tal que
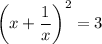
. Determine o valor da expressão

.
Notei que

.
Fiz o seguinte desenvolvimento:
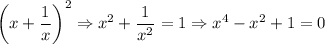
Então fiz uma substituição de variável,

, porém não possui raiz real e não consegui resolver. Depois pensei em continuar o desenvolvimento abaixo e encontrar o valor de
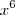
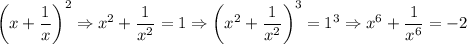
A partir daqui não consegui resolver
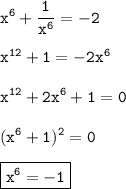
Por fim, basta vc substituir...
matmatco escreveu:Notei que

.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Seg Dez 16, 2024 20:44
por DanielFerreira » Seg Dez 16, 2024 20:44
matmatco escreveu:Seja x ∈ C não nulo tal que
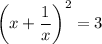
. Determine o valor da expressão

.
Notei que

.
Fiz o seguinte desenvolvimento:
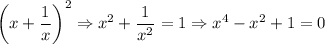
Então fiz uma substituição de variável,

, porém não possui raiz real e não consegui resolver. Depois pensei em continuar o desenvolvimento abaixo e encontrar o valor de
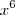
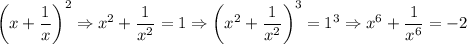
A partir daqui não consegui resolver
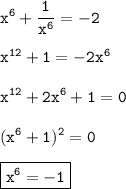
Por fim, basta vc substituir...
matmatco escreveu:Notei que
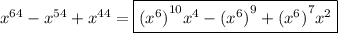
.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- matematica basica (produto notavel)
por Fabricio dalla » Sáb Mar 26, 2011 22:21
- 1 Respostas
- 1492 Exibições
- Última mensagem por Pedro123

Sáb Mar 26, 2011 23:18
Álgebra Elementar
-
- [Produto notavel com Radiciaçao(Polinômios)]
por Fabricio dalla » Qui Dez 08, 2011 13:11
- 1 Respostas
- 2270 Exibições
- Última mensagem por MarceloFantini

Qui Dez 08, 2011 22:00
Polinômios
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4942 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- Limite Notável-Como provar?
por joaofonseca » Dom Out 30, 2011 20:19
- 4 Respostas
- 4056 Exibições
- Última mensagem por joaofonseca

Ter Nov 01, 2011 08:14
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite notável
por Nicolas1Lane » Sáb Set 28, 2013 13:13
- 4 Respostas
- 2801 Exibições
- Última mensagem por Nicolas1Lane

Sáb Set 28, 2013 18:22
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
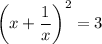 . Determine o valor da expressão
. Determine o valor da expressão  .
. .
.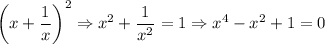
 , porém não possui raiz real e não consegui resolver. Depois pensei em continuar o desenvolvimento abaixo e encontrar o valor de
, porém não possui raiz real e não consegui resolver. Depois pensei em continuar o desenvolvimento abaixo e encontrar o valor de 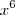
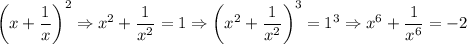


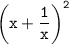

 , afinal como
, afinal como  depois era só aplicar a
depois era só aplicar a 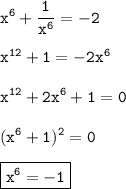
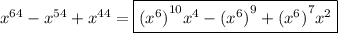 .
.