


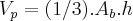

 area da base,
area da base, altura e base respectivamente...
altura e base respectivamente...
![{l}^{2}={2}^{2}+2^2=8\Rightarrow l=2.\sqrt[]{2}
{A}_{b}={l}^{2}={(2.\sqrt[]{2})}^{2}=8... {l}^{2}={2}^{2}+2^2=8\Rightarrow l=2.\sqrt[]{2}
{A}_{b}={l}^{2}={(2.\sqrt[]{2})}^{2}=8...](/latexrender/pictures/083829b50084756195cd8f50a988d3db.png)
![x=\sqrt[]{(2.\sqrt[]{2})^2-(3/2)^2}=\sqrt[]{8-(9/4)} x=\sqrt[]{(2.\sqrt[]{2})^2-(3/2)^2}=\sqrt[]{8-(9/4)}](/latexrender/pictures/d743c3cca872f22a3b3550cd790abbc1.png)
![\sqrt[]{2}... \sqrt[]{2}...](/latexrender/pictures/92f8b9302ed14c65b3537c898831d81b.png)
![x=\sqrt[]{23/4}=\sqrt[]{23}/2... x=\sqrt[]{23/4}=\sqrt[]{23}/2...](/latexrender/pictures/1688a6d3c08f3956f20c01f7a02228a8.png)
![{x}^{2}={h}^{2}+{\sqrt[]{2}}^{2}\Rightarrow h=\sqrt[]{(\sqrt[]{(23}/2))^2-2}
h=\sqrt[]{(23/4)-2)}=\sqrt[]{15}/2...
{V}_{p}=(1/3).{A}_{b}.h=(1/3).8.\sqrt[]{15}/2=(4/3)\sqrt[]{15}... {x}^{2}={h}^{2}+{\sqrt[]{2}}^{2}\Rightarrow h=\sqrt[]{(\sqrt[]{(23}/2))^2-2}
h=\sqrt[]{(23/4)-2)}=\sqrt[]{15}/2...
{V}_{p}=(1/3).{A}_{b}.h=(1/3).8.\sqrt[]{15}/2=(4/3)\sqrt[]{15}...](/latexrender/pictures/b027b7357980bbe3ccde5df2916ca2f5.png)

![x=\sqrt[]{23}/2 x=\sqrt[]{23}/2](/latexrender/pictures/e47a516db990fda27f146e259d02a562.png) nao é o segmento que une o vertice ao lado do quadrado,perpendicular a esse,e sim a outra aresta lateral...entao,vamos calcular esse segmento(chamaremos de y...).usando o criterio de semelhança LAL,teremos
nao é o segmento que une o vertice ao lado do quadrado,perpendicular a esse,e sim a outra aresta lateral...entao,vamos calcular esse segmento(chamaremos de y...).usando o criterio de semelhança LAL,teremos![y/(\sqrt[]{23}/2)=1.5/2\sqrt[]{2}=(3/2)/2\sqrt[]{2}
\Rightarrow y=(3/8).\sqrt[]{23}... y/(\sqrt[]{23}/2)=1.5/2\sqrt[]{2}=(3/2)/2\sqrt[]{2}
\Rightarrow y=(3/8).\sqrt[]{23}...](/latexrender/pictures/15d76a347d6a0cd869d1f16e67728837.png)
![y=(3/8).\sqrt[]{23},l=\sqrt[]{2},h y=(3/8).\sqrt[]{23},l=\sqrt[]{2},h](/latexrender/pictures/6a3f3a5d7b47bdf65ed548391b881fd7.png) ,determinaremos h.usando pitagoras teremos
,determinaremos h.usando pitagoras teremos![h=\sqrt[]{{((3/8).\sqrt[]{23}})^{2}-{(\sqrt[]{2}})^{2}}
h=\sqrt[]{79/64}=\sqrt[]{79}/8 h=\sqrt[]{{((3/8).\sqrt[]{23}})^{2}-{(\sqrt[]{2}})^{2}}
h=\sqrt[]{79/64}=\sqrt[]{79}/8](/latexrender/pictures/05e613c5308f861564624f6c3d72abb6.png)
![{V}_{p}=(1/3).8.(\sqrt[]{79}/8)=\sqrt[]{79}/3... {V}_{p}=(1/3).8.(\sqrt[]{79}/8)=\sqrt[]{79}/3...](/latexrender/pictures/21229594f32ed84b841692a7218d39a6.png)

Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.