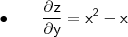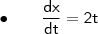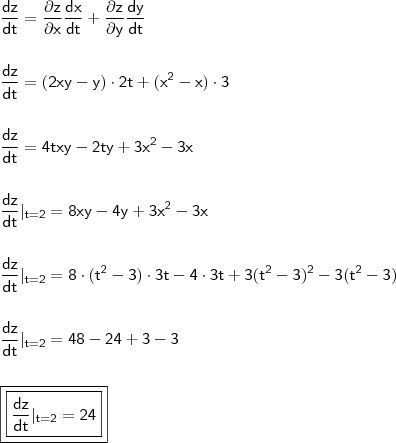por Guga1981 » Qua Nov 11, 2020 02:22
por Guga1981 » Qua Nov 11, 2020 02:22
Bom dia, amigos!
Faço Licenciatura em Matemática na Univesp.
Gosto de assistir as video-aulas pausando os exercícios e resolvendo-os antes de ver a resposta.
Ao tentar fazer o exercício abaixo, a minha solução deu diferente da do professor.
Gostaria de uma opinião de vocês para eu saber se fiz certo e o professor se equivocou (às vezes acontece...) ou o contrário.
Segue o exercício (a minha resposta deu -12 e a do professor +24):
A temperatura em uma superfície é dada por z=f(x,y)= x²y - xy. Uma partícula se desloca sobre esta superfície pela curva γ(t)=(t²-3, 3t) [onde (t²-3) é a coordenada x(t) e 3t é a coordenada y(t)].
Determine a taxa de variação de temperatura, sofrida por esta partícula, no instante t=2.
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por Guga1981 » Sex Nov 13, 2020 10:44
por Guga1981 » Sex Nov 13, 2020 10:44
Consegui resolver! O professor estava certo!
-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
 por DanielFerreira » Sex Nov 20, 2020 14:15
por DanielFerreira » Sex Nov 20, 2020 14:15
A taxa de variação da temperatura será dada por

, onde

,

e
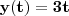
.
Daí, temos que:

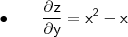
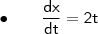

Substituindo,
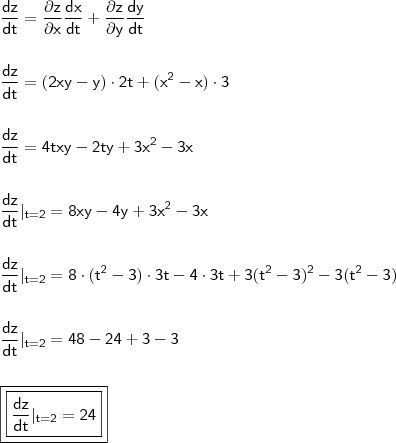
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Guga1981 » Dom Nov 22, 2020 05:02
por Guga1981 » Dom Nov 22, 2020 05:02
Obrigado!

-
Guga1981
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Dom Jan 18, 2015 13:27
- Localização: São Vicente-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo de várias variáveis] Problema de regra da cadeia
por Hoteri » Seg Dez 05, 2016 23:56
- 1 Respostas
- 5170 Exibições
- Última mensagem por adauto martins

Qui Dez 08, 2016 09:09
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo para Funções de Várias Variáveis I
por ehrefundini » Ter Abr 29, 2008 23:16
- 1 Respostas
- 5886 Exibições
- Última mensagem por Neperiano

Dom Set 04, 2011 22:28
Pedidos de Materiais
-
- Regra da Cadeia 3 Variaveis Urgente
por Silva339 » Ter Mar 19, 2013 22:27
- 2 Respostas
- 2549 Exibições
- Última mensagem por Silva339

Qua Abr 03, 2013 18:24
Cálculo: Limites, Derivadas e Integrais
-
- calculos para funçoes de varias variaveis
por flavio970 » Sex Out 16, 2015 22:25
- 0 Respostas
- 3494 Exibições
- Última mensagem por flavio970

Sex Out 16, 2015 22:25
Cálculo para Funções de Várias Variáveis II
-
- [Integrais] Regra da cadeia para antidiferenciação
por MrJuniorFerr » Sáb Out 27, 2012 20:02
- 6 Respostas
- 4790 Exibições
- Última mensagem por MrJuniorFerr

Dom Out 28, 2012 01:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , onde
, onde  ,
,  e
e 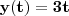 .
.