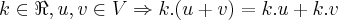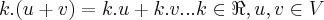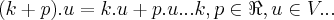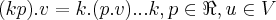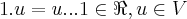2.mostre que o conjunto de combinações lineares das variáveis x e y é um espaço vetorial com operações usuais
Combinações lineares de x e y formam o conjunto dos elementos u = ax + by
A1 associativa u + (v + w) = (u + v) + w
ax + by + (cx + dy + ex + fy) = ax + by + cx + dy + ex + fy = (ax + by + cx + dy) + ex + fy
Alguém pode me ajudar? Gostaria de saber se estar correto, e quais passos devo seguir. ( Estou estudando por conta, e sou leiga)


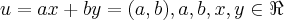 }
}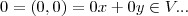 e p/quaquer
e p/quaquer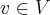
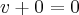
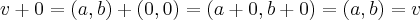
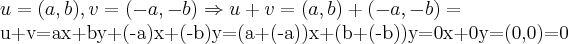

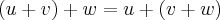
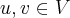
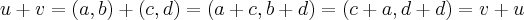
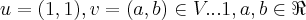
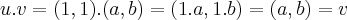

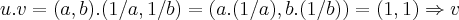 é o elemento inverso multplicativo de u...
é o elemento inverso multplicativo de u...