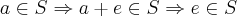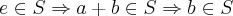por adauto martins » Dom Dez 29, 2019 18:13
por adauto martins » Dom Dez 29, 2019 18:13
uma algebra é definida por (S,+),onde S é um conjunto e "+" o operador soma dos elementos de S.
mostre que:
a)existe o operador multiplicativo " * ".
b)existe o elemento neutro da soma,e o elemento unidade do operador multiplicativo.
c)existe o elemento simetrico da soma e o elemento neutro multiplicativo.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Dom Dez 29, 2019 18:50
por adauto martins » Dom Dez 29, 2019 18:50
a)
seja
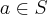
,entao pela definiçao da algebra,teremos:

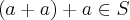
.
.
.
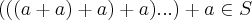
essa soma contada b vezes sera
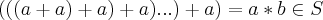
,logo
existe o operador " * ",dito multiplicativo em S.
b)
o elemento neutro da soma,tera que satisfazer a:

pela definiçao da algebra,teremos:
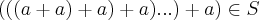
,contado "e" vezes,e

,logo
existe "

racionio analogo,mostra-se que existe o elemento unidade do operdor multiplicativo
que deve satisfazer a condiçao

(faça-o como exercicio)
c)
usando racionio analogo ao exposto acima termine-o!
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Dez 30, 2019 12:11
por adauto martins » Seg Dez 30, 2019 12:11
ps-desconsidere a demonstraçao da letra b),pois esta ficou imprecisa,indeterminada...vale para mostrar que sempre existe um elemento em S,cuja soma esta em S.mas nao precisou o elemento que em nosso caso é o elemento neutro da soma.geralmente nos livros de algebra,esses elementos entram como definiçao dada pelo autor.mas sao de suma importancia para o desenvolver da teroria,em especifico,teoria dos numeros.quando eu tiver a forma precisa de mostrar tais elementos,eu a posto,no mais,obrigado...adauto martins
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Jan 03, 2020 17:33
por adauto martins » Sex Jan 03, 2020 17:33
resolverei as letras b) e c) de forma muito elementar,mas concisa...
b)´

como
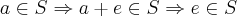

como

c)

como mostramos acima que existe o elemento neutro do operador soma "e",entao
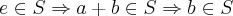
o inverso do operador multiplicativo fica como exercicio...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- algebra l
por ehrefundini » Qui Mar 05, 2009 08:34
- 1 Respostas
- 7468 Exibições
- Última mensagem por Molina

Qui Mar 05, 2009 21:50
Álgebra
-
- algebra
por uspsilva » Sex Mar 13, 2009 13:03
- 1 Respostas
- 3212 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 15:22
Pedidos
-
- Algebra
por mattheusramos14 » Ter Ago 03, 2010 01:26
- 1 Respostas
- 2749 Exibições
- Última mensagem por MarceloFantini

Ter Ago 03, 2010 13:37
Álgebra Elementar
-
- ALGEBRA
por JOHNY » Sex Set 03, 2010 23:50
- 1 Respostas
- 2714 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:12
Álgebra Elementar
-
- álgebra
por Eliana Fidelis » Dom Out 24, 2010 13:52
- 1 Respostas
- 2658 Exibições
- Última mensagem por Adriano Tavares

Ter Mar 08, 2011 20:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


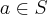 ,entao pela definiçao da algebra,teremos:
,entao pela definiçao da algebra,teremos:
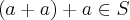
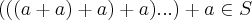
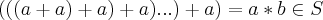 ,logo
,logo
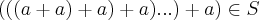 ,contado "e" vezes,e
,contado "e" vezes,e ,logo
,logo
 (faça-o como exercicio)
(faça-o como exercicio)