soluçao:
o problema pede as raizes racionais,ou seja as raizes da forma (p/q),onde p,q sao primos entre si.
em um polinomio a forma de encontrar as possiveis raizes racionas é dado por:
os divisores p,de

, e os divisores q, de

.aqui inclui os positivos e negativos
logo
div(12)=[-12,-6,-4,-3,-2,-1,1,2,3,4,6,12]
div(3)=[-3,-1,1,3]
as possiveis raizes racionais,(p/q)sao:
[-12,-6,-4,-3,-2,-1,-4/3,-2/3,-1/3,1/3,2/3,4/3,1,2,3,4,6,12]
sao 18 possibilidades de se achar uma,ou mais raizes racionais de p(x),que se faz via substituindo as possibilidades no polinomio,uma a uma(que tarefa,heim!...) e verificando a condiçao de p(x)=0.
aqui,p(1)=0,pois

bom,achando uma raiz,podemos entao diminuir o grau do polinomio

temos agora um polinomio de terceiro grau,a saber
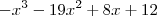
logo,faremos novamente o processo de possibilidades das raizes racionais para

possiveis raizes [-1,-2,-3,-4,-6,-12,1,2,3,4,6,12]
e procurarmos entre esses,uma ou mais valores que satisfaz a condiçao de r(x)=0...
como o polinomio inicial é de quatro grau,podemos ter 4 raizes,3 raizes(uma com multiplicidade 2),2 raizes(uma com multiplicidade 3,ou duas com multiplicidade 2),1 raiz(com multiplicidade 4)...bom,aos interessados termine-o...
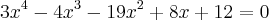

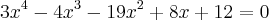

 , e os divisores q, de
, e os divisores q, de  .aqui inclui os positivos e negativos
.aqui inclui os positivos e negativos

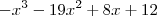


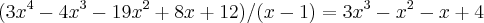


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.