vamos indepente da restriçao do dominio da funçao original,tomar o polinomio:

encontramos,de uma maneira suscinta,o intervalo de localizaçao das raizes(e tem diversos metodos para tal,e todos eficientes;um dos metodos mais eficiente é o de LAGUERRE,o qual vc usa p(x) e p(-x) e encontra as cotas superiores e inferiores...).no nosso caso achamos o intervalo[-3,3],para efeito de calculo rapido.
usaremos agora o teorema de bolzano(estude ai...),calculando:

logo
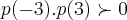
pelo teorema de bolzano,teremos um numero par de raizes reais,ou nenhuma...
se o produto

teriamos um numero impar de raizes.
agora usaremos o criterio de DESCARTES, das trocas de sinas de p(x) e p(-x)
em p(x) temos (+,+,-,-) uma troca,ou seja a possibilidade de termos uma raiz real positiva...
em p(-x) temos (+,-,+,-) duas trocas,ou seja a possiblidade de termos duas raizes negativas...
como ja mostramos que
 e teremos nunhuma ou um numero par de raizes.temos a seguite configuraçao:
e teremos nunhuma ou um numero par de raizes.temos a seguite configuraçao:podemos ter uma raiz positiva,uma raiz negativa ou duas raizes negativas e nenhuma positiva,pois como o polinomio é de quarto grau,podemos ter um par de raizes complexos-conjugado.pois nao existe uma so raiz complexa,e sim em pares de complexos-conjugados.um criterio para saber se ha raizes complexas é da pela "regra da lacuna" e 'regra de huat",que em suma diz:
se
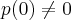 e se tomarmos algum
e se tomarmos algum 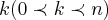
tivermos
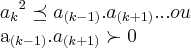
voltando ao nosso polinomio,teremos
![p(0)=-2\neq 0...
tomemos [tex]k=3...{{a}_{3}}^{2}={2}^{2}=4\succ ({a}_{4}.{a}_{2})=1.0=0 p(0)=-2\neq 0...
tomemos [tex]k=3...{{a}_{3}}^{2}={2}^{2}=4\succ ({a}_{4}.{a}_{2})=1.0=0](/latexrender/pictures/cab2f11dcba811cab63beaf947688dd9.png)
ou
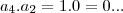 ,ou seja nao temos um par de complexos-conjugados.
,ou seja nao temos um par de complexos-conjugados.logo,poderemos ter ,pelo que frizamos ate o momento uma raiz real positiva e uma raiz real negativa,ou duas raizes negativas,ou nenhuma raiz...
encontra-las,se houver, faremos adiante,no momento eu queria fazer apenas essa pequena explanaçao...


 e para algum
e para algum 
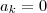 e
e  ,
, 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.