num triangulo ABC sao dados:
i)A(2,0)
ii)M(-1,4)ponto medio de AB
iii)
iv)
![{d}_{BC}=10\sqrt[]{2}](/latexrender/pictures/62b6a540fe20ef64c973519c2c26d026.png "{d}_{BC}=10\sqrt[]{2}")
obter o vertice C do triangulo.
por adauto martins » Sáb Out 19, 2019 01:08
por adauto martins » Seg Out 21, 2019 12:47
![{d}_{AC}=\sqrt[]{{(x-2)}^{2}+{y}^{2}}=10(1)
{d}_{BC}=\sqrt[]{{(x+4)}^{2}+{(y-8)}^{2}}=10\sqrt[]{2}(2)](/latexrender/pictures/cb14da3ea0f9dc7cd64727b1d0000778.png "{d}_{AC}=\sqrt[]{{(x-2)}^{2}+{y}^{2}}=10(1)
{d}_{BC}=\sqrt[]{{(x+4)}^{2}+{(y-8)}^{2}}=10\sqrt[]{2}(2)")
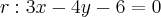
e substituindo em (2),teremos:![\sqrt[]{{(x+4)}^{2}+{((3x-6)/4)-8)}^{2}}=10\sqrt[]{2}](/latexrender/pictures/6cafebfea95ba8dfe95ace3f8de2c7f5.png "\sqrt[]{{(x+4)}^{2}+{((3x-6)/4)-8)}^{2}}=10\sqrt[]{2}")
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)