soluçao:
pegando "um gancho",como se diz,na questao anteriormente resolvida,da escola quimica,vamos resolver esse da politecnica de sao paulo.o raciocinio e similiar.
ps-esses vestibulares antigos,ditos exames de admissao,das escolas,universidades das ares de exata,como as engenharia,como posso ver cobravam muito,versando em geometria e polinomios.
voltemos ao exercicio,o qual pede-se a distancia x,da esfera,tal que determine uma fraçao de (1/m) da superficie da esfera.
a area de superficie de uma esfera ,como um todo e dado por:
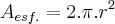
,onde r e o raio da esfera.queremos determinar a area das coltas q. sao (1/m) da area superficial dessa esfera,ou seja:
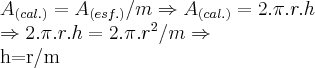
,onde h e o ponto do plano de corte da calota ao ponto externo da esfera,que esteja na reta q. une,o ponto P(pontode luz),k ponto de intersecçao da reta com o plano de corte e O,centro da esfera.
como no exerc. anterior(escola de quimica),teremos 2 triangulos retangulos semelhantes que sao o PTO,pKT...
fazendo as devidas proporçoes teremos:
sabendo que
![PT=\sqrt[]{{(x+r)}^{2}+{r}^{2}} PT=\sqrt[]{{(x+r)}^{2}+{r}^{2}}](/latexrender/pictures/fd56eca167f337e34c0708fcd5b2e5ad.png)
...

agora e isolar x,sabendo que h=r/m...termine-o...


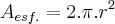 ,onde r e o raio da esfera.queremos determinar a area das coltas q. sao (1/m) da area superficial dessa esfera,ou seja:
,onde r e o raio da esfera.queremos determinar a area das coltas q. sao (1/m) da area superficial dessa esfera,ou seja: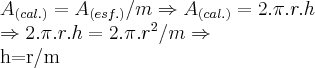 ,onde h e o ponto do plano de corte da calota ao ponto externo da esfera,que esteja na reta q. une,o ponto P(pontode luz),k ponto de intersecçao da reta com o plano de corte e O,centro da esfera.
,onde h e o ponto do plano de corte da calota ao ponto externo da esfera,que esteja na reta q. une,o ponto P(pontode luz),k ponto de intersecçao da reta com o plano de corte e O,centro da esfera.![PT=\sqrt[]{{(x+r)}^{2}+{r}^{2}} PT=\sqrt[]{{(x+r)}^{2}+{r}^{2}}](/latexrender/pictures/fd56eca167f337e34c0708fcd5b2e5ad.png) ...
...