1) Assinale a alternativa correta :
( ) Se f é decrescente em seu domínio, então a derivada que de f é negativa em todos os pontos de seu domínio.
( ) Se a derivada segunda de f é positiva em um intervalo e negativa em outro, então f possui um ponto de inflexão.
( )Se f é crescente em seu domínio, então a derivada de f é positiva em um intervalo e negativa em outro, então f não possui ponto de inflexão.
( )A função
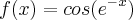 possui uma assíntota horizontal.
possui uma assíntota horizontal.Resposta da ultima derivada
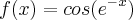
Utilizo a regra da cadeia u = f(g(x)) -> y'=(g(x)). g'(x)
f(x) cos = sen
f(x)
 =
= 
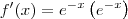 ( Não sei se está certo também )
( Não sei se está certo também )2) Considere a seguinte situação: o raio e altura de um cilindro estão variando de modo que seu volume não se altera.
( )A taxa de variação da altura e raio são constantes.
( ) A área total do cilindro está aumentando.
( ) A área da superfície do cilindro também se mantém constante.
( )Se a altura está aumentando, a taxa de variação da altura do cilindro é maior que a taxa de variação do raio do cilindro.
3)Considere a função
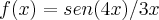
( ) A função f é uma função ímpar.
( ) A função f é uma função par.
( ) A função f possui uma assíntota vertical.
( ) A função f possui uma assíntota horizontal.
Resolvendo a derivada
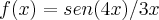
Derivo utilizando a regra da cadeia u = f(g(x)) -> y'=(g(x)). g'(x)
f'(x) sen = cos
f'(x) 4x = 4
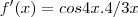
Gostaria de saber se essa resposta está correta e que me ajudem a saber qual opção ela é.
4)Considere a função

( ) Existem pontos no gráfico e nos quais a reta tangente é horizontal.
( ) A função f possui um número par de pontos críticos.
( )Como a derivada de f é negativa em todo seu domínio, a função f é uma função decrescente.
( ) O Gráfico f possui um ponto de inflexão.
Resolvendo a derivada

Primeiro aplico a regra do expoente


Aplico a regra
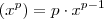
E obtenho o resultado:

Agora a parte de fazer os gráficos eu não sei muito bem
5) Esboce o gráfico da função

explicitando o domínio da função, os interceptos (casos existam) com os e
ixos, as assíntotas (caso existam),
estudo do crescimento/decrescimento e estudo da concavidade da função.




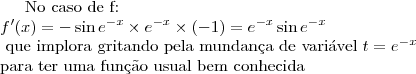

![\begin{array}{rl} \mathcal{D}_{\!f}=\mathbb{R}^*\\f'(x)&=\dfrac{((\cos{4x})\times 4)\times (3x) - (\sin{4x}) \times (3)}{(3x)^2}\\[\bigskipamount]&=\dfrac{4x\cos{4x}-\sin{4x}}{3x^2}\end{array} \begin{array}{rl} \mathcal{D}_{\!f}=\mathbb{R}^*\\f'(x)&=\dfrac{((\cos{4x})\times 4)\times (3x) - (\sin{4x}) \times (3)}{(3x)^2}\\[\bigskipamount]&=\dfrac{4x\cos{4x}-\sin{4x}}{3x^2}\end{array}](/latexrender/pictures/5aa595a096fa98884ca5f90f629e6a22.png)




 e também que se
e também que se  é uma função derivável e não-nula então
é uma função derivável e não-nula então  . Não precisa passar pela derivada de uma potência.
. Não precisa passar pela derivada de uma potência. deve estar em algum lugar nos seus livros de aula.
deve estar em algum lugar nos seus livros de aula.




