brumadense escreveu:Olá colegas
Gostaria de uma explicação de como essa função foi resolvida. Estou sentindo dificuldade em resolver funções quando aparecem com radicais. Alguém poderia me explicar como resolver quando aparece radicais, como no caso abaixo? Desde já agradeço.
Seja a função
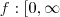
)

R dado por f
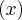
=
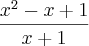
. Calcule:
![f \left(\sqrt[2]{2}-1 \right)=\frac{{\left(\sqrt[2]{2}-1 \right)}^{2}-\left(\sqrt[2]{2}-1 \right)+1}{\sqrt[2]{2}-1+1}=\frac{2-2\sqrt[2]{2}+1-\sqrt[2]{2}+1+1}{\sqrt[2]{2}}=\frac{5-3\sqrt[2]{2}}{\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-3\sqrt[2]{2}.\sqrt[2]{2}}{\sqrt[2]{2}.\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-6}{2} f \left(\sqrt[2]{2}-1 \right)=\frac{{\left(\sqrt[2]{2}-1 \right)}^{2}-\left(\sqrt[2]{2}-1 \right)+1}{\sqrt[2]{2}-1+1}=\frac{2-2\sqrt[2]{2}+1-\sqrt[2]{2}+1+1}{\sqrt[2]{2}}=\frac{5-3\sqrt[2]{2}}{\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-3\sqrt[2]{2}.\sqrt[2]{2}}{\sqrt[2]{2}.\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-6}{2}](/latexrender/pictures/02315716053abca173ab996ed26fafef.png)
Bom dia.
Dada esta função
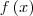
=
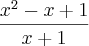
queremos encontrar
![f \left(\sqrt[2]{2}-1 \right) f \left(\sqrt[2]{2}-1 \right)](/latexrender/pictures/90d35ea6766006e5e36ab952c432473a.png)
, ou seja, vamos substituir todos os x da equação por
![\sqrt[2]{2}-1 \sqrt[2]{2}-1](/latexrender/pictures/f04f8b4ee7780eec1f1bd142c7b476fd.png)
. E foi isso que foi feito.
Os procedimentos seguintes foi só algebrismo. Elevar ao quadrado, somar, subtrair, etc. Porém, o denominador da fração (parte de baixo) ficou com raiz. Quando isso acontece temos que racionalizar esta fração, ou seja, eliminar essa raiz de baixo. Para fazer isso o truque é sempre o mesmo: multiplicar pela própria raiz. Só que temos que multiplicar em cima e embaixo. E foi isso que foi feito, multiplicando por

.
Qualquer dúvida, avise!

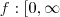 )
) R dado por f
R dado por f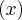 =
=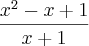 . Calcule:
. Calcule:![f \left(\sqrt[2]{2}-1 \right)=\frac{{\left(\sqrt[2]{2}-1 \right)}^{2}-\left(\sqrt[2]{2}-1 \right)+1}{\sqrt[2]{2}-1+1}=\frac{2-2\sqrt[2]{2}+1-\sqrt[2]{2}+1+1}{\sqrt[2]{2}}=\frac{5-3\sqrt[2]{2}}{\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-3\sqrt[2]{2}.\sqrt[2]{2}}{\sqrt[2]{2}.\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-6}{2} f \left(\sqrt[2]{2}-1 \right)=\frac{{\left(\sqrt[2]{2}-1 \right)}^{2}-\left(\sqrt[2]{2}-1 \right)+1}{\sqrt[2]{2}-1+1}=\frac{2-2\sqrt[2]{2}+1-\sqrt[2]{2}+1+1}{\sqrt[2]{2}}=\frac{5-3\sqrt[2]{2}}{\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-3\sqrt[2]{2}.\sqrt[2]{2}}{\sqrt[2]{2}.\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-6}{2}](/latexrender/pictures/02315716053abca173ab996ed26fafef.png)


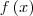 =
=![f \left(\sqrt[2]{2}-1 \right) f \left(\sqrt[2]{2}-1 \right)](/latexrender/pictures/90d35ea6766006e5e36ab952c432473a.png) , ou seja, vamos substituir todos os x da equação por
, ou seja, vamos substituir todos os x da equação por ![\sqrt[2]{2}-1 \sqrt[2]{2}-1](/latexrender/pictures/f04f8b4ee7780eec1f1bd142c7b476fd.png) . E foi isso que foi feito.
. E foi isso que foi feito. .
.


 .
.
 :
: