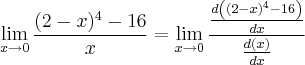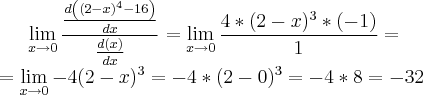por Therodrigou » Qua Jun 20, 2018 06:46
por Therodrigou » Qua Jun 20, 2018 06:46
Olá! o que deve fazer, na expressão a seguir, para que ela seja igual a -32
[(2-x)^4-16]/x
quando X tende a 0
Obrigado pela atenção!
-
Therodrigou
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Jun 20, 2018 06:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia mecânica
- Andamento: cursando
 por Gebe » Qua Jun 20, 2018 18:35
por Gebe » Qua Jun 20, 2018 18:35
Ja que substituindo o 0 (zero) na expressão obtemos uma indeterminação 0/0, podemos utilizar a regra de l'Hopital.
Assim o LIMITE da expressão é igual ao da expressão com o numerador e o denominador derivados, ou seja:
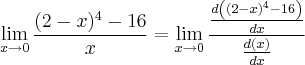
Resolvendo então temos:
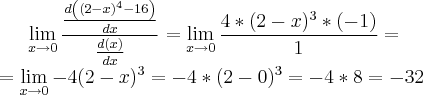
Espero ter ajudado, se ficar alguma duvida na resolução mande msg.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Therodrigou » Qua Jun 20, 2018 22:54
por Therodrigou » Qua Jun 20, 2018 22:54
vlw!
-
Therodrigou
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Jun 20, 2018 06:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia mecânica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7257 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- Provar lim f(x)g(x) =0 quando o x tende a p
por Danilct » Seg Dez 07, 2015 22:00
- 0 Respostas
- 2223 Exibições
- Última mensagem por Danilct

Seg Dez 07, 2015 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [Matemática Básica] Qual o valor de -X² quando x vale...
por Nando26 » Sex Jun 04, 2021 12:53
- 3 Respostas
- 11024 Exibições
- Última mensagem por DanielFerreira

Ter Jun 22, 2021 16:32
Equações
-
- [LIMITE] Limite que tende ao infinito
por Mell » Qua Mai 08, 2013 00:09
- 3 Respostas
- 2619 Exibições
- Última mensagem por e8group

Qua Mai 08, 2013 21:21
Cálculo: Limites, Derivadas e Integrais
-
- Quando saber que não existe um limite ?
por OtavioBonassi » Qua Jan 05, 2011 15:14
- 6 Respostas
- 52587 Exibições
- Última mensagem por OtavioBonassi

Qua Jan 05, 2011 19:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.