 por liviatoniolo222 » Dom Mai 06, 2018 22:58
por liviatoniolo222 » Dom Mai 06, 2018 22:58
Eu fiz essa questões de todas as maneiras possíveis e só consegui chegar ao resultado de 968690,9401242 porém a resposta correta é 968,690.
O que eu estou fazendo de errado?
1/ 6,28 x 0,8 x10^3 x 205,478 x10^-12
-
liviatoniolo222
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mai 06, 2018 22:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: eletromecanica
- Andamento: cursando
 por Gebe » Dom Mai 06, 2018 23:16
por Gebe » Dom Mai 06, 2018 23:16
Primeiramente a forma como tu colocou a expressão está confusa.
Dessa forma como está escrito é equivalente a:
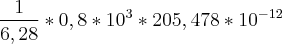
Porem pelo resultado deve ser:
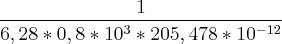
Sendo assim, realmente a tua conta está certa. Para bater com o gabarito falta um 1000 multiplicando no denominador, logo ou o gabarito está errado mesmo ou (uma possibilidade) o exercicio esta utilizando a virgula do 205,478 em outra notação, ou seja, é na verdade 205478 ou ainda o gabarito está apresentado neste tipo de notação (virgula separando os milhares das centenas).
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por liviatoniolo222 » Dom Mai 06, 2018 23:38
por liviatoniolo222 » Dom Mai 06, 2018 23:38
Gebe escreveu:Primeiramente a forma como tu colocou a expressão está confusa.
Dessa forma como está escrito é equivalente a:
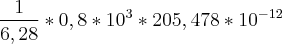
Porem pelo resultado deve ser:
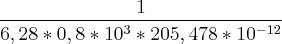
Sendo assim, realmente a tua conta está certa. Para bater com o gabarito falta um 1000 multiplicando no denominador, logo ou o gabarito está errado mesmo ou (uma possibilidade) o exercicio esta utilizando a virgula do 205,478 em outra notação, ou seja, é na verdade 205478 ou ainda o gabarito está apresentado neste tipo de notação (virgula separando os milhares das centenas).
- Anexos
-

- Segue em em anexo à questão. Usando 205478 eu consigo chegar ao resultado de 968,960
-
liviatoniolo222
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mai 06, 2018 22:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: eletromecanica
- Andamento: cursando
 por liviatoniolo222 » Dom Mai 06, 2018 23:45
por liviatoniolo222 » Dom Mai 06, 2018 23:45
Gebe escreveu:Primeiramente a forma como tu colocou a expressão está confusa.
Dessa forma como está escrito é equivalente a:
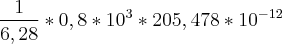
Porem pelo resultado deve ser:
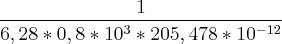
Sendo assim, realmente a tua conta está certa. Para bater com o gabarito falta um 1000 multiplicando no denominador, logo ou o gabarito está errado mesmo ou (uma possibilidade) o exercicio esta utilizando a virgula do 205,478 em outra notação, ou seja, é na verdade 205478 ou ainda o gabarito está apresentado neste tipo de notação (virgula separando os milhares das centenas).
Então, acabei de perceber que no circuito eu tenho 205.478 mas na solução está 205,478. Talvez por isso a confusão de valores.
-
liviatoniolo222
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mai 06, 2018 22:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: eletromecanica
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- preciso urgente DE FORMULAS PRA EU RESOLVER OU RESULTADOS DE
 por Eder » Seg Jun 23, 2008 14:19
por Eder » Seg Jun 23, 2008 14:19
- 1 Respostas
- 3003 Exibições
- Última mensagem por Molina

Seg Jun 23, 2008 17:56
Matemática Financeira
-
- Probabilidade - Confirmar resultados Urgentee
por Suy Becker » Qua Mai 11, 2011 15:04
- 0 Respostas
- 8490 Exibições
- Última mensagem por Suy Becker

Qua Mai 11, 2011 15:04
Estatística
-
- [Probabilidade] dos Resultados de Poliedros com 12 Faces
por Red » Ter Abr 17, 2018 03:34
- 0 Respostas
- 4760 Exibições
- Última mensagem por Red

Ter Abr 17, 2018 03:34
Probabilidade
-
- Possibilidade de resultados em 4 jogos com 15 possibilidades
por FellipeMaoski » Seg Abr 17, 2017 01:21
- 0 Respostas
- 2845 Exibições
- Última mensagem por FellipeMaoski

Seg Abr 17, 2017 01:21
Análise Combinatória
-
- [Dúvida sobre resultados de pesquisa] Amostragem
por gutsownz » Qua Out 17, 2018 13:08
- 0 Respostas
- 6112 Exibições
- Última mensagem por gutsownz

Qua Out 17, 2018 13:08
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



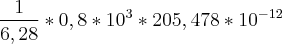
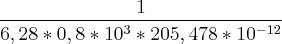





 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.