 em que o gradiente de
em que o gradiente de  tem módulo máximo?
tem módulo máximo?a)(0,-1) e (0,1)
b)(-1,0) e (1,0)
c)(-?2/2 , - ?2/2) e (?2/2, ?2/2)
d)(1,0) e (0,1)
e)(-1,0) e (0,-1)
Fiz o gradiente de F(x,y)=(x,2y), mas não sei como continuar para chegar nesse resultado.
O gabarito é letra A.
Se alguém puder me ajudar ficarei muito grato.


 tem sempre o mesmo valor(pq?)...
tem sempre o mesmo valor(pq?)...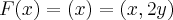 ...
... são ortogonais(pq?),logo:
são ortogonais(pq?),logo: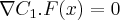
 ...a solução da intersecao das circunf.teremos:
...a solução da intersecao das circunf.teremos: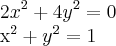


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)