Regra da poligonal e Regra do Paralelogramo

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Regra da poligonal e Regra do Paralelogramo

Regras do fórum
Responder

Regra da poligonal e Regra do Paralelogramo

Mensagempor fernando7 » Qui Abr 12, 2018 22:22

Qual a diferença?
Anexos
1.png
fernando7
Usuário Ativo
Usuário Ativo
 
Mensagens: 14
Registrado em: Qua Abr 11, 2018 20:31
Formação Escolar: ENSINO FUNDAMENTAL II
Andamento: cursando
Voltar ao topo

Re: Regra da poligonal e Regra do Paralelogramo

Mensagempor Gebe » Sex Abr 13, 2018 00:49

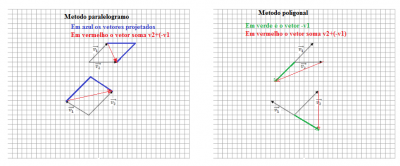
A diferença mais interessante, na minha opniao, é que o metodo poligonal permite somar (ou subtrair) mais de 2 vetores por vez, enquanto o metodo do paralelogramo permite a soma (ou sub) de apenas dois vetores, ou seja, se tivermos mais de 2 vetores o segundo metodo terá de ser aplicado mais de uma vez.

http://osmatematicos.com.br/docs/vetoresgeometrico.pdf

Nesta pagina (pdf) que eu coloquei entre as paginas 15 e 21 são explicados muito bem os dois metodos, incluindo exemplos. Preferi botar esta pagina, ja que esta materia depende muito de desenhos, portanto fica dificil fazer uma boa explicação aqui.
No youtube também, caso prefira, tem bons videos sobre.

Em anexo coloco a resolução do exercicio pelos dois metodos.
Anexos
1.png
Gebe
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 158
Registrado em: Qua Jun 03, 2015 22:47
Formação Escolar: GRADUAÇÃO
Área/Curso: engenharia eletrica
Andamento: cursando
Voltar ao topo
Responder

Voltar para Álgebra Linear

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: Princípio da Indução Finita
Autor: Fontelles - Dom Jan 17, 2010 14:42

Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?
2n \geq n+1 ,\forall n \in\aleph*
O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois 2.1 \geq 1+1
2°) Admitamos que P(k), k \in \aleph*, seja verdadeira:
2k \geq k+1 (hipótese da indução)
e provemos que 2(k+1) \geq (K+1)+1
Temos: (Nessa parte)
2(k+1) = 2k+2 \geq (k+1)+2 > (k+1)+1

Assunto: Princípio da Indução Finita
Autor: MarceloFantini - Seg Jan 18, 2010 01:55

Boa noite Fontelles.

Não sei se você está familiarizado com o Princípio da Indução Finita, portanto vou tentar explicar aqui.

Ele dá uma equação, no caso:

2n \geq n+1, \forall n \in \aleph^{*}

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

2*1 \geq 1+1

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que k seja verdadeiro, e pretendemos provar que também é verdadeiro para k+1.

\mbox{Suponhamos que P(k), }k \in \aleph^{*},\mbox{ seja verdadeiro:}
2k \geq k+1

\mbox{Vamos provar que:}
2(k+1) \geq (k+1)+1

Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.

Espero ter ajudado.

Um abraço.

Assunto: Princípio da Indução Finita
Autor: Fontelles - Seg Jan 18, 2010 02:28

Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!

Assunto: Princípio da Indução Finita
Autor: Fontelles - Qui Jan 21, 2010 11:32

Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.

Assunto: Princípio da Indução Finita
Autor: MarceloFantini - Qui Jan 21, 2010 12:25

Boa tarde Fontelles!

Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.

O que temos que provar é isso: 2(k+1) \geq (k+1)+1, certo? O autor começou do primeiro membro:

2(k+1)= 2k+2

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

2k+2 \geq (k+1)+2

Que é outra verdade. Agora, com certeza:

(k+1)+2 > (k+1)+1

Agora, como 2(k+1) é \geq a (k+1)+2, e este por sua vez é sempre > que (k+1)+1, logo:

2(k+1) \geq (k+1)+1 \quad \mbox{(c.q.d)}

Inclusive, nunca é igual, sempre maior.

Espero (dessa vez) ter ajudado.

Um abraço.

Assunto: Princípio da Indução Finita
Autor: Caeros - Dom Out 31, 2010 10:39

Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?

Assunto: Princípio da Indução Finita
Autor: andrefahl - Dom Out 31, 2010 11:37

c.q.d. = como queriamos demonstrar =)

Assunto: Princípio da Indução Finita
Autor: Abelardo - Qui Mai 05, 2011 17:33

Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.

Assunto: Princípio da Indução Finita
Autor: MarceloFantini - Qui Mai 05, 2011 20:05

Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.

Assunto: Princípio da Indução Finita
Autor: Vennom - Qui Abr 26, 2012 23:04

MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.

Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa. :-D

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum