Olá, simplesmente não consigo entender o seguinte enunciado, e estou muito curioso para saber a resposta:
''Aplicando a definição de logaritmo, encontre o maior número a , inteiro, e o menor número b, inteiro, tais que a < log 5 < b. ''
10^x=5
x=0,69...
O que eu devo fazer agora para achar a e b, assumindo que até estou correto?
a < 0,69... < b ?
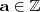, então deve determinar o inteiro mais próximo de 0,69 e menor que ele; ZERO.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)