1° Questão
Dados os conjuntos A={a,b,c,d} e B={5,6,7,8,9}, o número de arranjos simples 5 a 5 que podemos formar com os elementos desses dois conjuntos, de maneira que nesses arranjos tenha sempre 2 letras, é igual a:
a)240 b)1440 c)2880 d)7200
OBS: Tentei resolver com principio fundamental da contagem, mantendo 2 letras fixas e analisando as possibilidades nos espaços restantes e depois permutar estas duas letras, mas não consegui executar!
2° Questão
Uma pessoa pretende levar para casa 8 pacotes de um determinado produto de um supermercado. Se no supermercado tem 6 marcas diferentes desse produto e ela quer provar de todas essas marcas, de quantas maneiras diferentes ela poderá levar esses produtos?
OBS: Fiz um arranjo A8,6 mas não consegui chegar no resultado, o que fiz de errado?



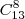


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)