[Valor Desconhecido em Uma Sentença] O Caso do Hotel

[ShadowOnLine]

Enunciado:
Durante uma viagem, um ônibus parou num hotel para os passageiros pernoitarem.
A diária dos homens custou o dobro da diária das mulheres, e estas pagaram o triplo da diária das crianças.
A despesa final foi de R$ 1.950,00.
Sabendo-se que eram 20 homens, 15 mulheres e 30 crianças, deseja-se saber quanto pagou cada criança, cada mulher e cada homem.





Resolução:
Chamaremos de "a" o valor pago pelas crianças, assim teremos que as mulheres pagaram "3a" que é triplo do valor das crianças, e os homens pagaram "6a" que é o dobro do valor das mulheres, e temos a expressão:





O enunciado ainda informa o número de pessoas, que eram 30 crianças, 15 mulheres e 20 homens. E aqui podemos inserir esses valores na expressão acima, e daí propomos:





Igualando a expressão ao valor total, e seguindo para a resolução, calculamos:





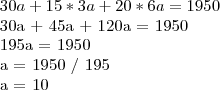
Então cada criança pagou R$ 10,00 e cada mulher pagou R$ 30,00 e cada homem pagou R$ 60.

Como havia 30 crianças, 15 mulheres e 20 homens, confirmamos:

10 x 30 crianças = 300
30 x 15 mulheres = 450
60 x 20 homens = 1200

Confirmando o total gasto: R$ 1.950,00

[DanielFerreira]

Olá! Não ficou clara a pretensão do tópico, mas a resolução está correta!

[ShadowOnLine]

Na verdade, eu tinha uma dúvida, mas enquanto eu escrevia a minha resolução - e aquela do outro tópico - eu entendi o que estava acontecendo, e como já havia digitado, resolvi enviar, imaginando que a resolução poderia ajudar alguém de alguma forma.

[DanielFerreira]

Certamente, irá ajudar alguém!