 por my2009 » Sex Jan 28, 2011 21:37
por my2009 » Sex Jan 28, 2011 21:37
O número real a é o menor dentre os valores de x que satisfazem a equação
![2{log}_{2} ( 1+\sqrt[]{2}x)-{log}_{2}(\sqrt[]{2x} )= 3 2{log}_{2} ( 1+\sqrt[]{2}x)-{log}_{2}(\sqrt[]{2x} )= 3](/latexrender/pictures/f8c450cae86ab19dac6b6041cd166294.png)
Então,
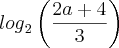
é igual a :
Resp 1/2
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por 0 kelvin » Sáb Jan 29, 2011 18:54
por 0 kelvin » Sáb Jan 29, 2011 18:54
Começa utilizando a propriedade do log de potência. 2 log a = log

Depois como tem subtração de log de base 2, reescreve como quociente.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por my2009 » Seg Jan 31, 2011 20:24
por my2009 » Seg Jan 31, 2011 20:24
Olá Kelvin... tentei fazer mas não deu certo mesmo
eu parei aqui :
![\frac{{log}_{2}(1 + \sqrt[]{2x})^2}{{log}_{2}(\sqrt[]{2x}) = 3} \frac{{log}_{2}(1 + \sqrt[]{2x})^2}{{log}_{2}(\sqrt[]{2x}) = 3}](/latexrender/pictures/9fa2ba1fea7902aa7cd1e9e024da4149.png)
rsrsrs vc pode terminaar

???
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por my2009 » Qua Fev 09, 2011 10:24
por my2009 » Qua Fev 09, 2011 10:24
alguem pode me ajudar ?
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por 0 kelvin » Qua Fev 09, 2011 11:39
por 0 kelvin » Qua Fev 09, 2011 11:39
!
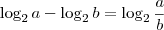
Eu devia ter dito propriedade do log quociente no lugar de "reescreve como quociente"

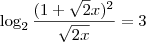
É raiz de 2 ou raiz de 2x em cima? Desenvolvendo a expressão esta parecendo que tem uma equação quadrática.
Definição do log:
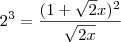
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por my2009 » Qua Fev 09, 2011 12:14
por my2009 » Qua Fev 09, 2011 12:14
Alguem , por favor pode responder essa questão ??? Desde o dia 28 DE JANEIRO estou esperando... e até então... não consegui resolver. 0 Kelvin agradeço sua ajuda.. mas estou ficando mais confusa hehehe desculpe
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Qua Fev 09, 2011 12:53
por DanielFerreira » Qua Fev 09, 2011 12:53
my2009,
confirma por favor
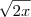
ou
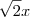
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por my2009 » Qua Fev 09, 2011 13:01
por my2009 » Qua Fev 09, 2011 13:01
Olá danjr5 é
![\sqrt[]{2} x \sqrt[]{2} x](/latexrender/pictures/6b2a0e264c2ba5308579a7798e89a972.png)
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Qua Fev 09, 2011 13:16
por DanielFerreira » Qua Fev 09, 2011 13:16
Consegui.
vou postar.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Qua Fev 09, 2011 13:36
por DanielFerreira » Qua Fev 09, 2011 13:36
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por my2009 » Qua Fev 09, 2011 15:45
por my2009 » Qua Fev 09, 2011 15:45
Com certeza ,me ajudou e muito !!!! Consegui entender... seria muito mais fácil se todas pessoas resolvessem dessa forma. Obrigada !
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Qui Fev 10, 2011 09:29
por DanielFerreira » Qui Fev 10, 2011 09:29
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Alisson Cabrini » Qui Ago 03, 2017 01:05
por Alisson Cabrini » Qui Ago 03, 2017 01:05
''
-
Alisson Cabrini
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Ago 03, 2017 00:53
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2571 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- Olha eu de novo...
por Fiel8 » Qua Jul 01, 2009 17:41
- 1 Respostas
- 3936 Exibições
- Última mensagem por Molina

Qua Jul 01, 2009 20:42
Funções
-
- MATRIZES DE NOVO
por GABRIELA » Ter Set 01, 2009 15:38
- 2 Respostas
- 4500 Exibições
- Última mensagem por profmatematica

Sáb Ago 28, 2010 05:34
Matrizes e Determinantes
-
- Geometria de Novo
por Ansso » Qui Out 21, 2010 22:31
- 11 Respostas
- 10625 Exibições
- Última mensagem por Ansso

Ter Out 26, 2010 20:43
Geometria Analítica
-
- ajuda eu de novo!!!!!
por zig » Sáb Fev 19, 2011 16:03
- 3 Respostas
- 4664 Exibições
- Última mensagem por LuizAquino

Sáb Fev 19, 2011 19:52
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![2{log}_{2} ( 1+\sqrt[]{2}x)-{log}_{2}(\sqrt[]{2x} )= 3 2{log}_{2} ( 1+\sqrt[]{2}x)-{log}_{2}(\sqrt[]{2x} )= 3](/latexrender/pictures/f8c450cae86ab19dac6b6041cd166294.png)
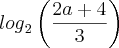 é igual a :
é igual a :
![2{log}_{2} ( 1+\sqrt[]{2}x)-{log}_{2}(\sqrt[]{2x} )= 3 2{log}_{2} ( 1+\sqrt[]{2}x)-{log}_{2}(\sqrt[]{2x} )= 3](/latexrender/pictures/f8c450cae86ab19dac6b6041cd166294.png)
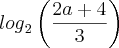 é igual a :
é igual a :


![\frac{{log}_{2}(1 + \sqrt[]{2x})^2}{{log}_{2}(\sqrt[]{2x}) = 3} \frac{{log}_{2}(1 + \sqrt[]{2x})^2}{{log}_{2}(\sqrt[]{2x}) = 3}](/latexrender/pictures/9fa2ba1fea7902aa7cd1e9e024da4149.png)
 ???
???

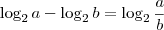

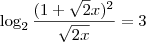 É raiz de 2 ou raiz de 2x em cima? Desenvolvendo a expressão esta parecendo que tem uma equação quadrática.
É raiz de 2 ou raiz de 2x em cima? Desenvolvendo a expressão esta parecendo que tem uma equação quadrática.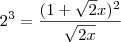


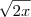 ou
ou 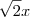

![\sqrt[]{2} x \sqrt[]{2} x](/latexrender/pictures/6b2a0e264c2ba5308579a7798e89a972.png)



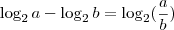 , temos
, temos![\log_{2} [\frac{(1 + \sqrt{2}x)^2}{\sqrt{2}x}] = 3 \log_{2} [\frac{(1 + \sqrt{2}x)^2}{\sqrt{2}x}] = 3](/latexrender/pictures/9e0418461a5d2d78dd7f825951b064a1.png)
![[\frac{(1 + 2.\sqrt{2}x + 2x^2}{\sqrt{2}x}] = 8 [\frac{(1 + 2.\sqrt{2}x + 2x^2}{\sqrt{2}x}] = 8](/latexrender/pictures/bc108fbce3e65c1f3e17bb1c7576b233.png)
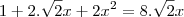


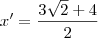
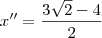
![\log_{2} [\frac{2a + 4}{3}] = \log_{2} [\frac{2a + 4}{3}] =](/latexrender/pictures/835cd68a58f44e8910a59ec875d47712.png)
![\log_{2} [\frac{2.\frac{3\sqrt{2} - 4}{2} + 4}{3}] = \log_{2} [\frac{2.\frac{3\sqrt{2} - 4}{2} + 4}{3}] =](/latexrender/pictures/e0d1f8a1ff959637f3ec699b26182a15.png)
![\log_{2} [\frac{3\sqrt{2} - 4 + 4}{3}] = \log_{2} [\frac{3\sqrt{2} - 4 + 4}{3}] =](/latexrender/pictures/b5898516437df32b654e198f467ddb44.png)
![\log_{2} [\frac{3\sqrt{2}}{3}] = \log_{2} [\frac{3\sqrt{2}}{3}] =](/latexrender/pictures/165e69d9727a69cb19e3bdfac11024d3.png)
![\log_{2} [\sqrt{2}] = \log_{2} [\sqrt{2}] =](/latexrender/pictures/6104a920f74808487ce4eab7a7c8cb1d.png)
![\log_{2} [2^\frac{1}{2}] = \log_{2} [2^\frac{1}{2}] =](/latexrender/pictures/82b89ffa57f2e06883465410c46d5f81.png)
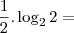








 .
.
 :
: